あけましておめでとうございます。
金輪際ポコ次郎です。

今年の目標は長生きじゃ

今年の目標は
虫歯にならないこと
突然ですが問題です。
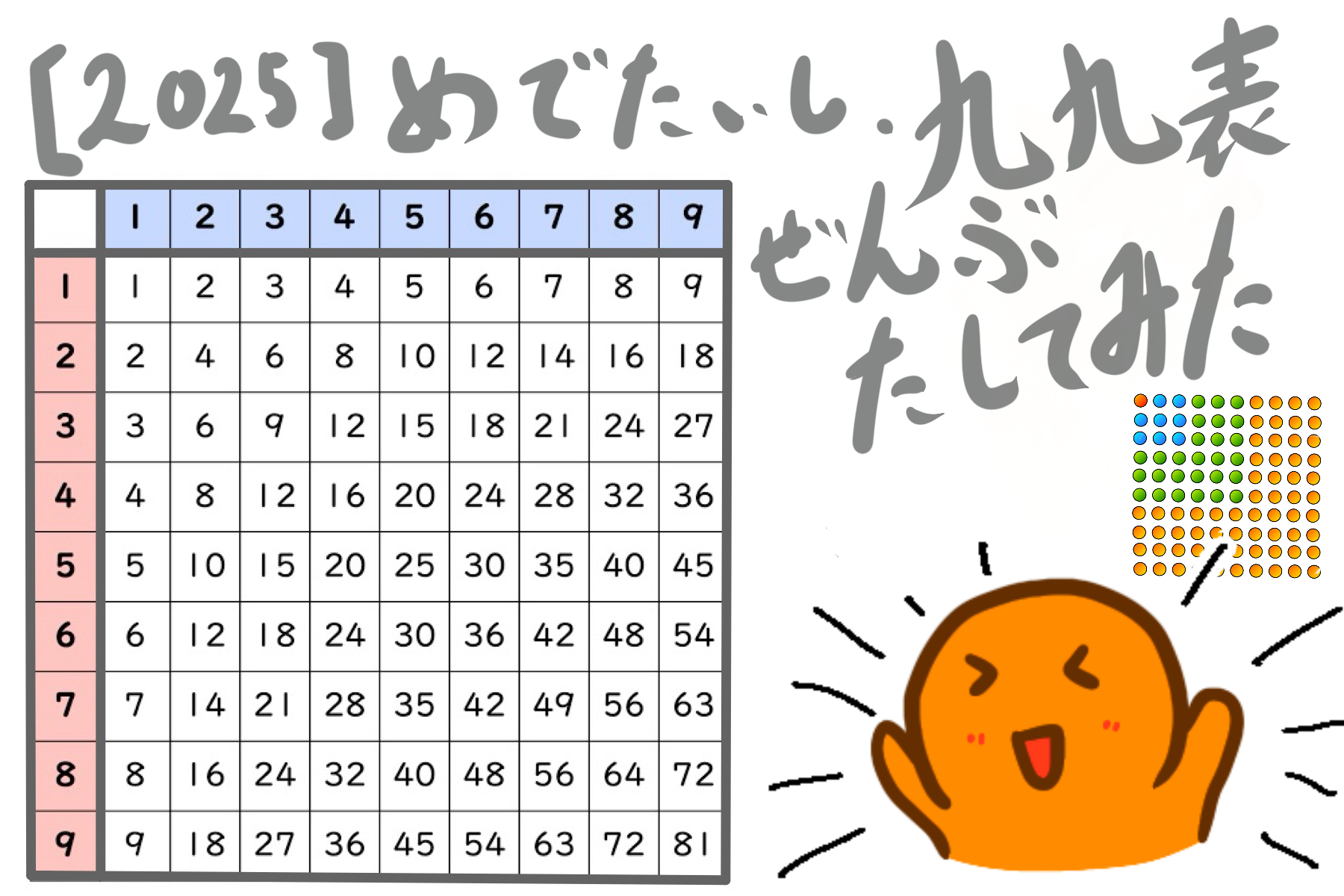
九九表の積(81こ)を
全部足したらいくつでしょう?
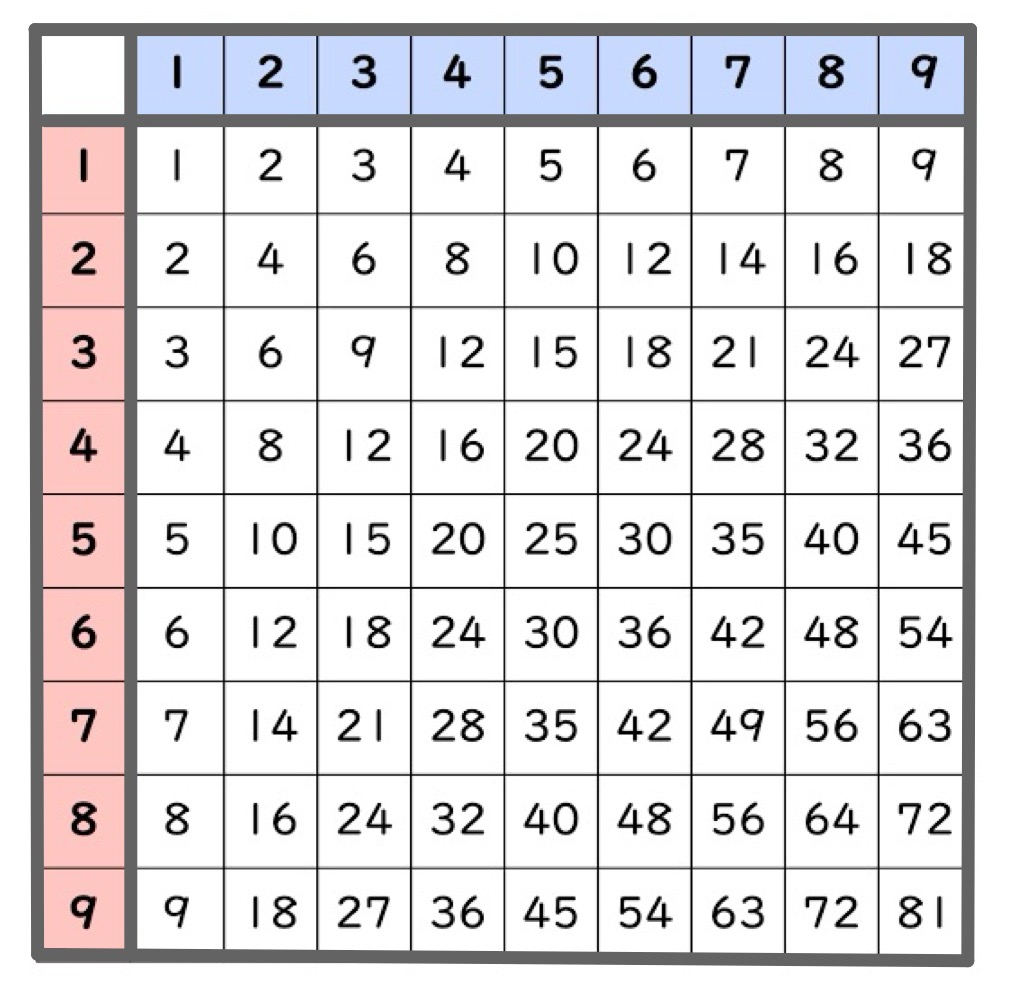

1の段〜9の段の答を
全部足すのじゃ!!

なにそれ超めんどい
本記事では、誰もが目にする九九表を、全部足したらいくつになるかを解説していきます。
おめでたい年明け記事ですので、晴れやかな気分でご覧ください。

それは読み手によるだろ
九九表の積、足してみた
①ガウスをリスペクト!
それぞれの段の和を考えます。
1の段
1+2+3+4+5+6+7+8+9
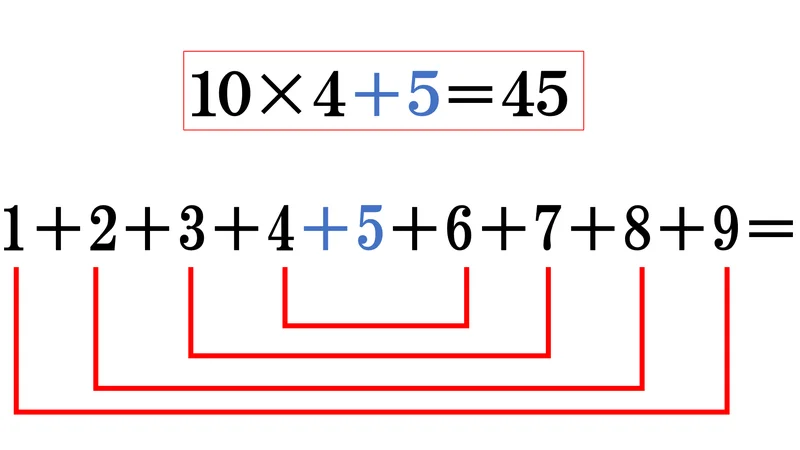
数学者ガウスは上のように考えたそうです。
ガウスをリスペクトすると、他の段も同じように考えられます。
2の段
2+4+6+8+10+12+14+16+18
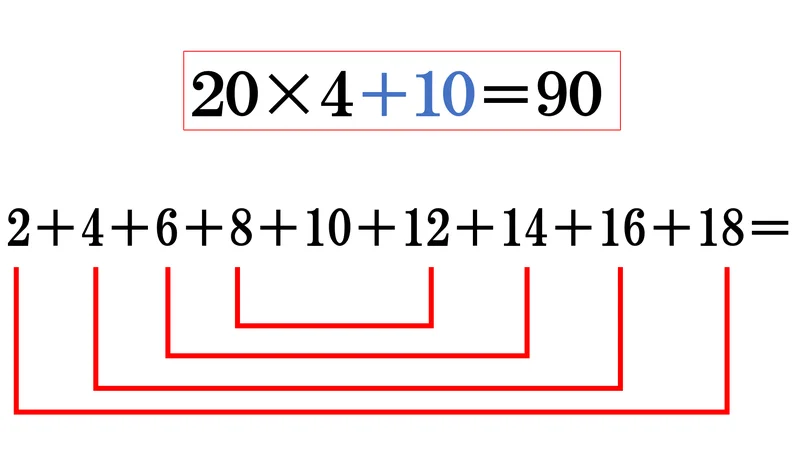
3の段
3+6+9+12+15+18+21+24+27
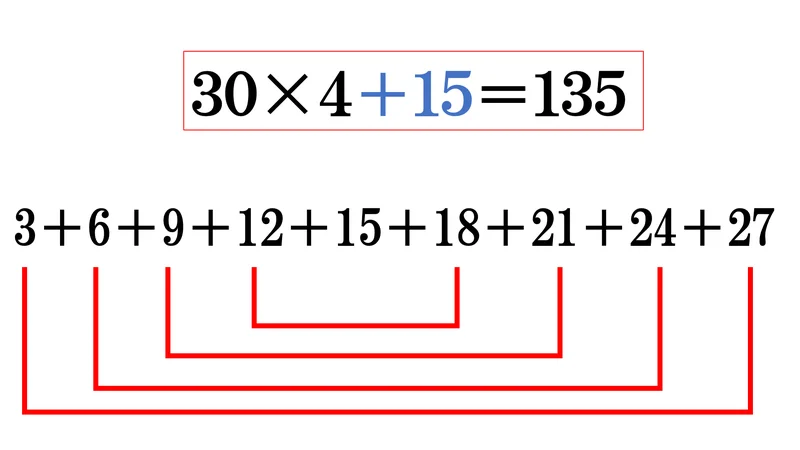

うわぁ
でもめんどくさいね
これでも全ての段の和を求めるのは大変です。
しかし、次のように考えるとどうでしょうか。
1の段
(1+2+3+4+5+6+7+8+9)
2の段
2+4+6+8+10+12+14+16+18
=(1+2+3+4+5+6+7+8+9)×2
3の段
3+6+9+12+15+18+21+24+27
=(1+2+3+4+5+6+7+8+9)×3
4の段
4+8+12+16+20+24+28+32+36
=(1+2+3+4+5+6+7+8+9)×4
・・・・・
9の段
9+18+27+36+45+54+63+72+81
=(1+2+3+4+5+6+7+8+9)×9
1〜9の段の和
(1+2+3+4+5+6+7+8+9)×(1+2+3+4+5+6+7+8+9)
=45×45
=2025

へー!すごい!
2025年になるね!

2025年ならではの
問題じゃのう
②100を見つけて!
次は九九表のおもしろさに目をつけて考えてみます。

九九表の四隅を足し算すると100になります。
1+9+9+81=100

へぇー、偶然
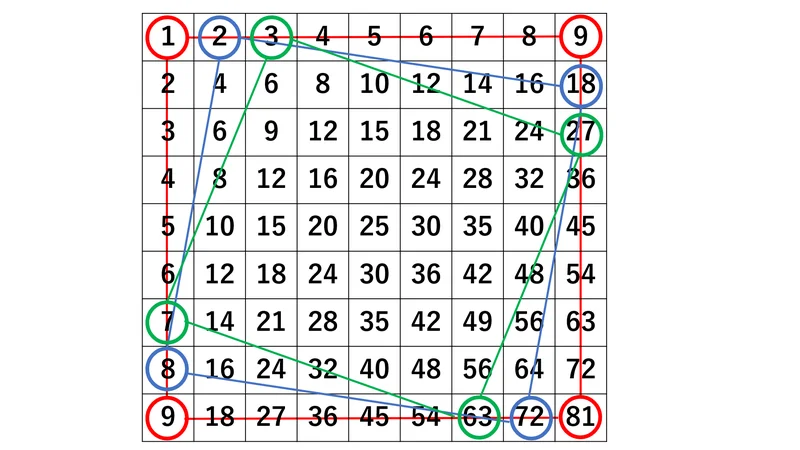
ちょっとずらして4つを足しても、
2+18+8+72=100
3+27+7+63=100

えーー!
すごい!なんでーー!
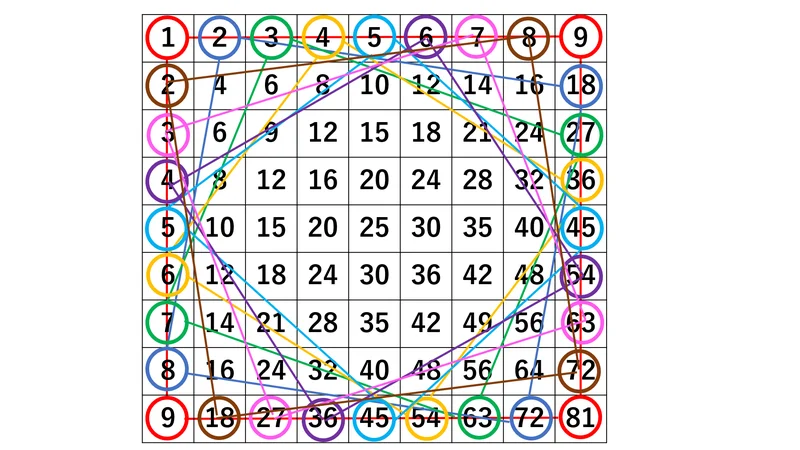
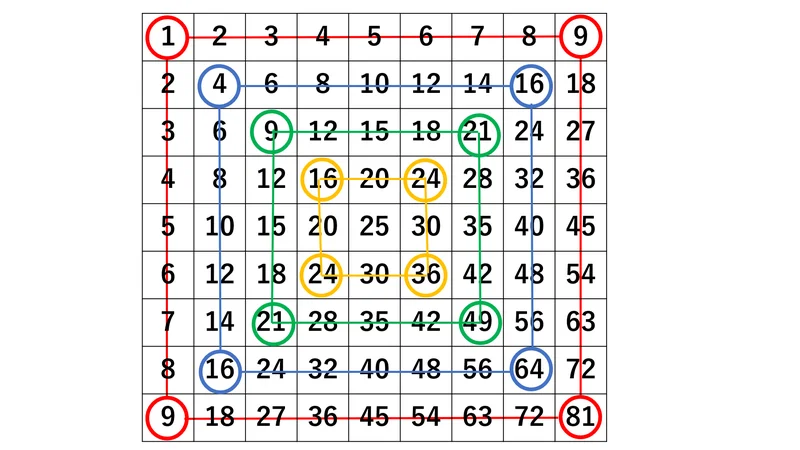
結んで正方形になる4点を結ぶと、これは必ず100になります。
80÷4点=20
つまり、100が20個できます。
中央の25が余りますので、九九表の和は、
100×20+25=2025
とわかります。

すごい…
九九表ってすごいよ…!

九九表の4点を結んで100に
なるのはおもしろいじゃろ
③立方数を伸ばす!
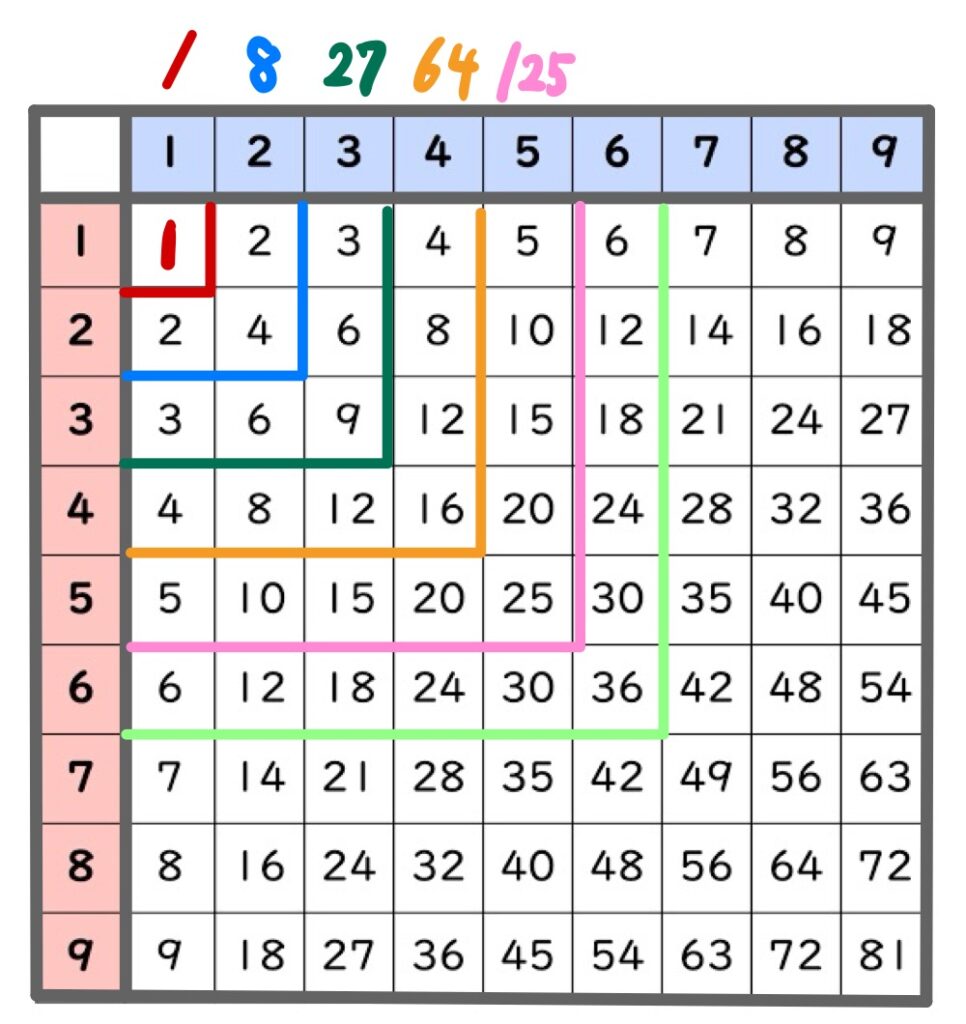
表を逆L字で区切ると、部分の和は
1、8、27、64…
と増えていきます。この数は立方数です。
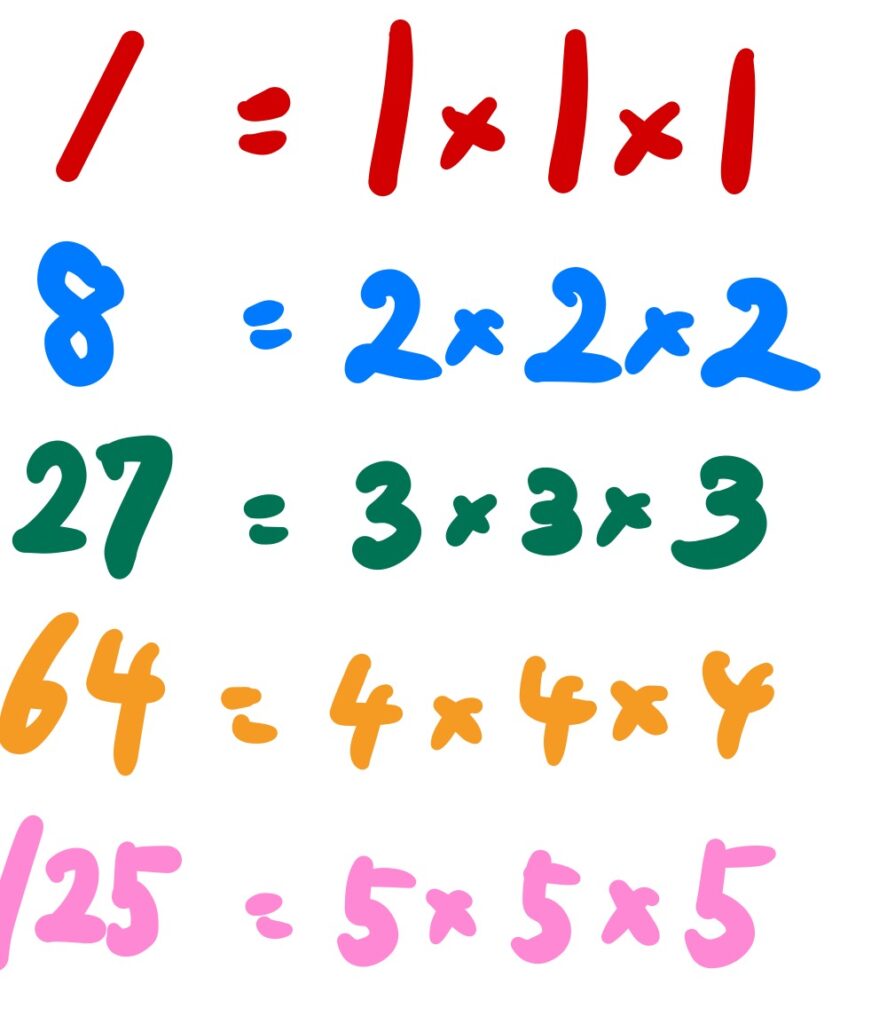
つまり、9段目までは、
1×1×1+2×2×2+3×3×3+…9×9×9
と考えられます。

いやいや、計算大変
すぎるでしょ

立方数は、平面に伸ばすのじゃ!
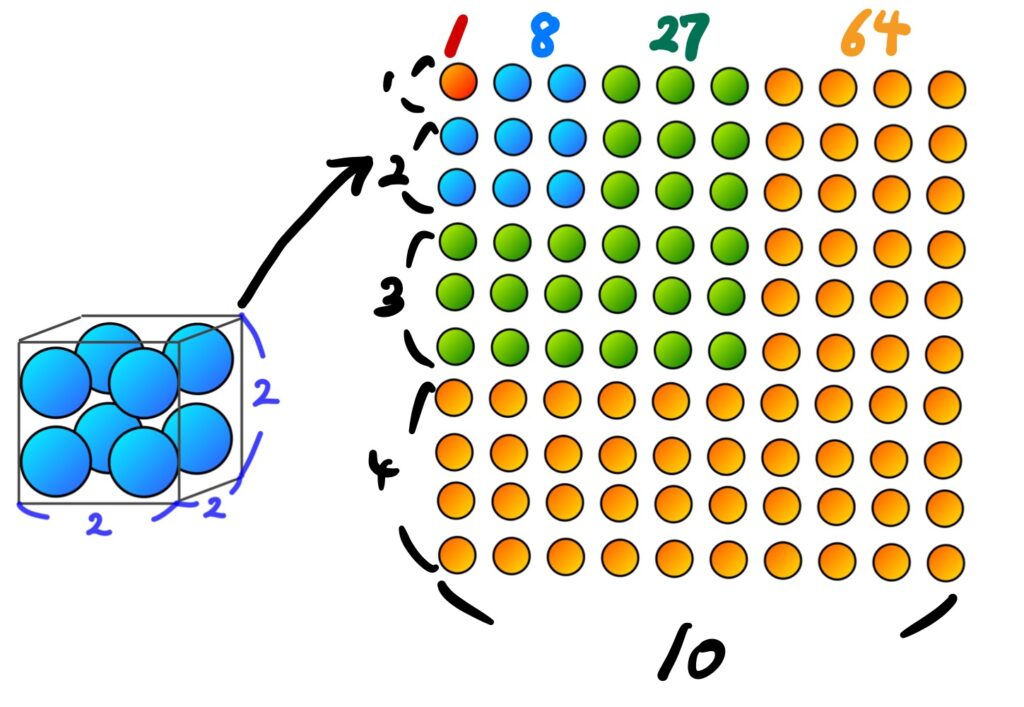
立方体の中にある球を、平面に伸ばすと考えてみます。
1×1×1+2×2×2+3×3×3+4×4×4
=(1+2+3+4)×(1+2+3+4)
=10×10
=100

なんだこの考え方は!
これを使うと、
1×1×1+2×2×2+3×3×3+…9×9×9
=(1+2+3+4+5+6+7+8+9)×(1+2+3+4+5+6+7+8+9)
=45×45
=2025
となりますね。

最初の式と同じだね

一つの問いにも、解き方は
たくさんあるのじゃよ!
今年は2025年。
45×45であり、九九表全てを足した数。
九九表の和の平均25が81個分でもあります。
いい年にしていきましょう。
それでは、ありがとうございました!



コメント