こんにちは、金輪際ポコ次郎です。
日本を世界一、算数好きな国にするために毎日頑張っています。
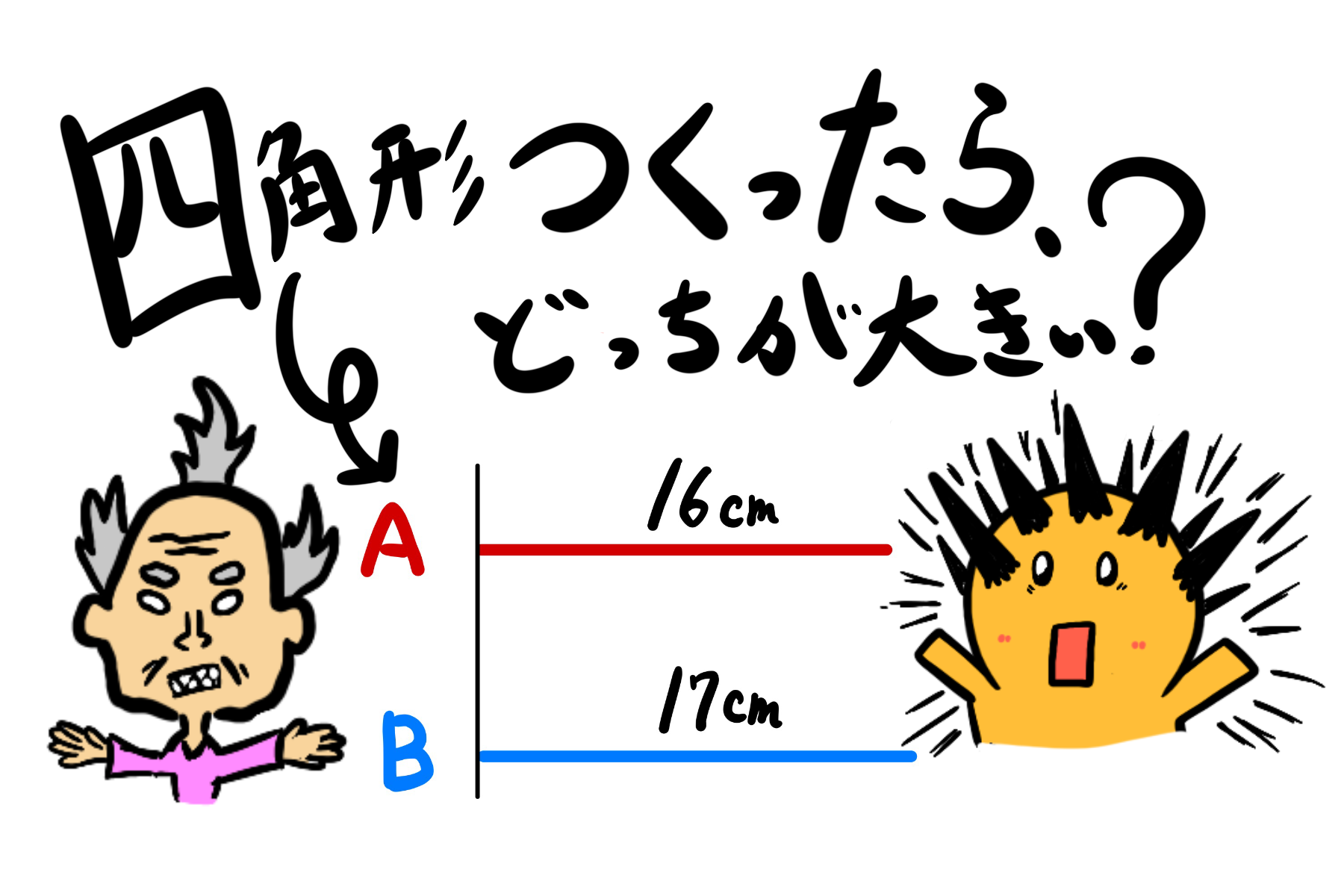
突然ですが、二つの紐があります。
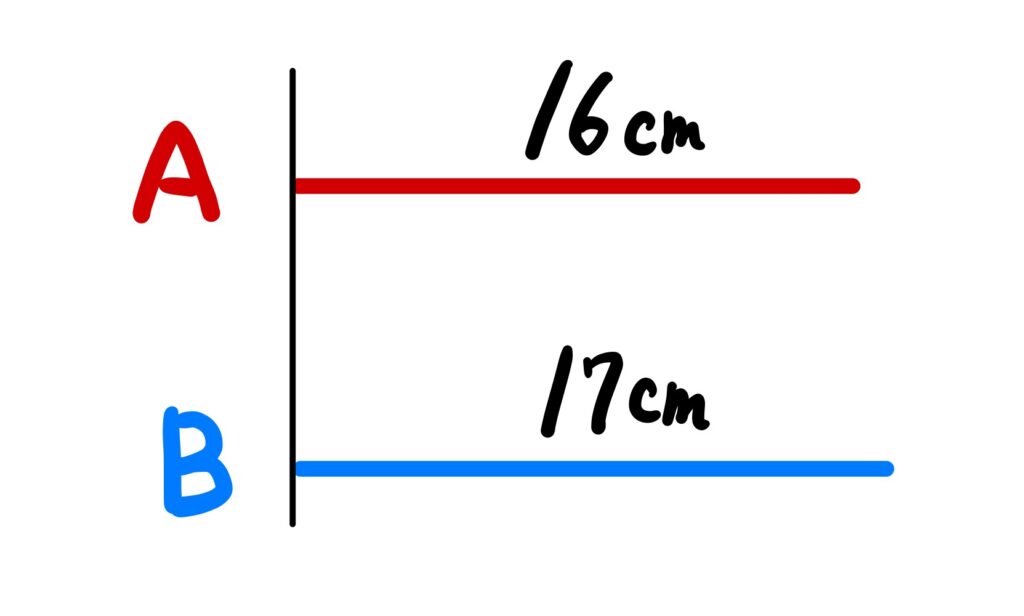
この紐をそれぞれ折り曲げて、四角形を作ります。
A、Bの四角形を同じ面積にして下さい。

いやいや!
Bの面積の方が大きいでしょ!

なぜそう思うんじゃ?

Bの紐の方が長いから、
できる四角形も大きいよ!

いい予想じゃ
でも、本当かのう?
長さの違う紐で同じ面積はできる?
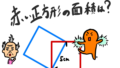
赤の面積は?
さて、まずは赤の面積を考えましょう。
16cmの紐でできる四角形の面積はいくつでしょうか。
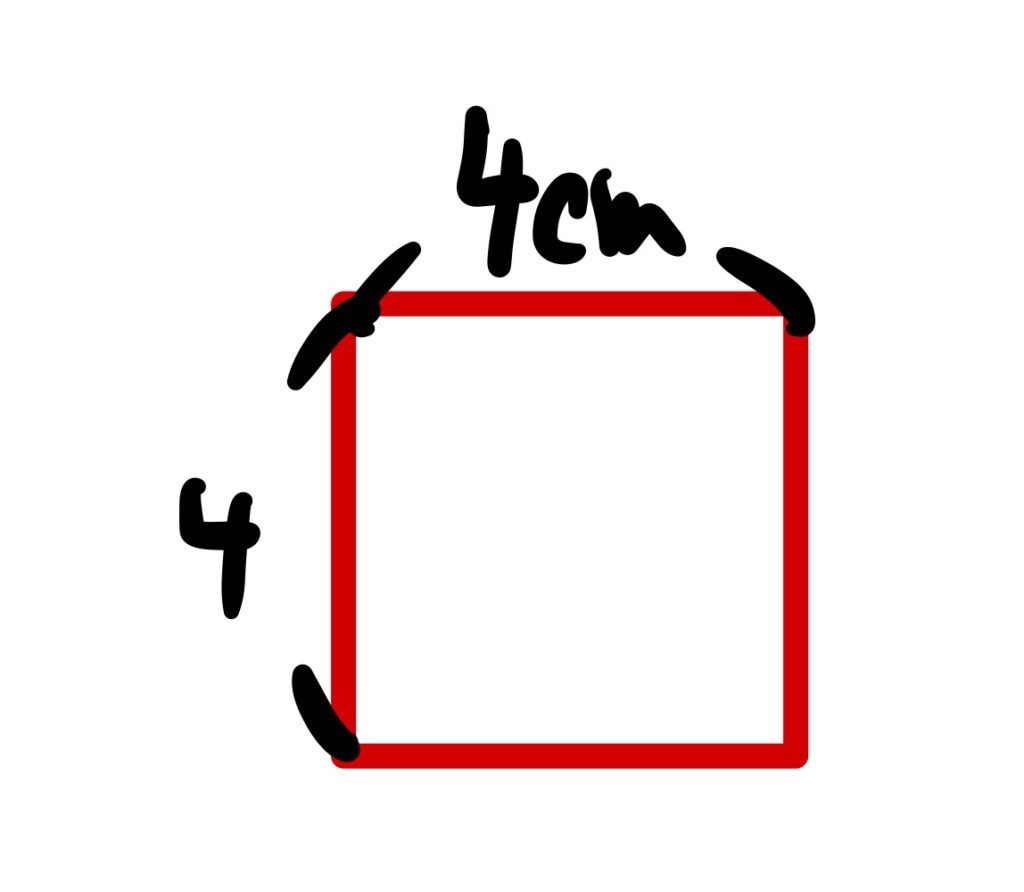

簡単だよ
一辺が4cmの正方形さ

それだけか?

なっ、なに!?

いつから四角形が正方形
だけと錯覚していた?
まず、16cmの紐からできる四角形はいくつかありますね。
(たて)+(よこ)=8
と、常に8で一定になります。
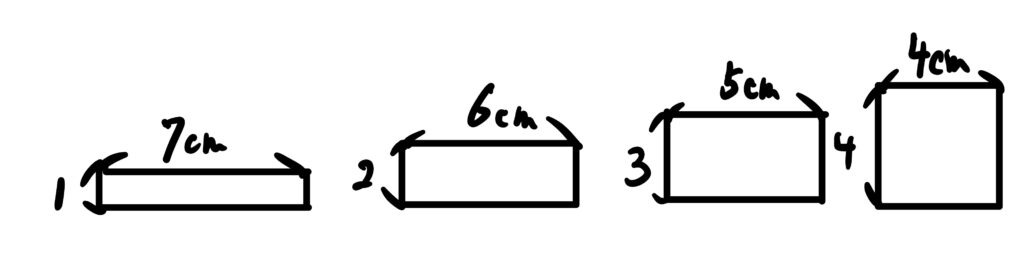
そして、それぞれ面積は変わります。
周りの長さが同じでも、形によって面積は変わるのです。
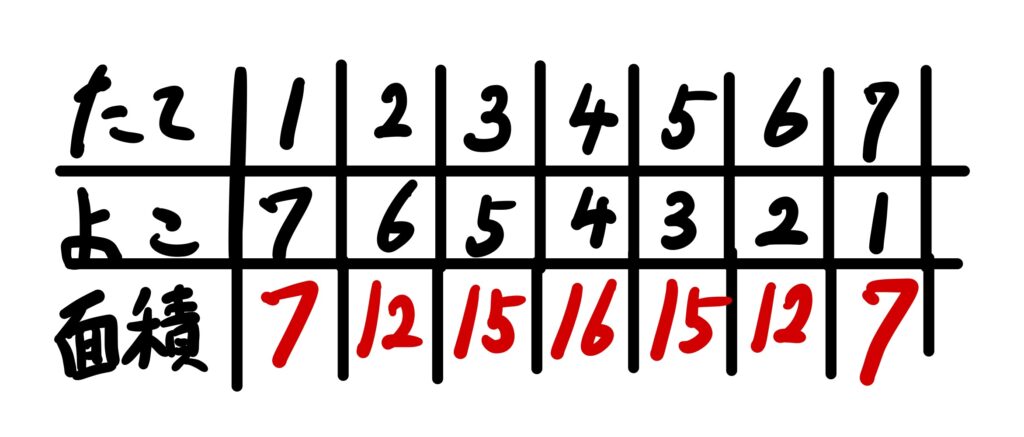
本来は形は無数にありますが、今回はたてを1〜7の整数にしました。このとき、面積は7㎠、12㎠、15㎠、16㎠の四通りとなりますね。

おお!
同じ紐でも面積が変わるんだ

意外じゃな
青の面積は?
青の紐でできる面積はいくつでしょうか?
青紐は17cmなので、
(たて)+(よこ)=8.5cm
になります。これも、形は無数にあります。
今回はたてを1〜8の整数にしました。
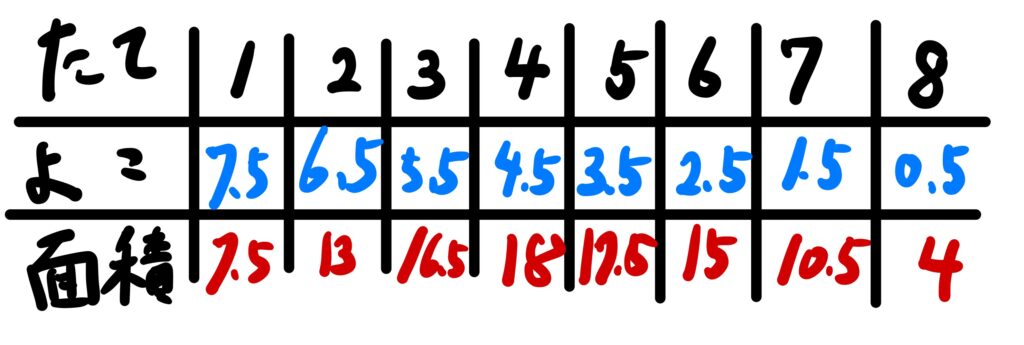

さて、同じ面積はあるかの?

そんな偶然あるわけ…
あるーーー!!!
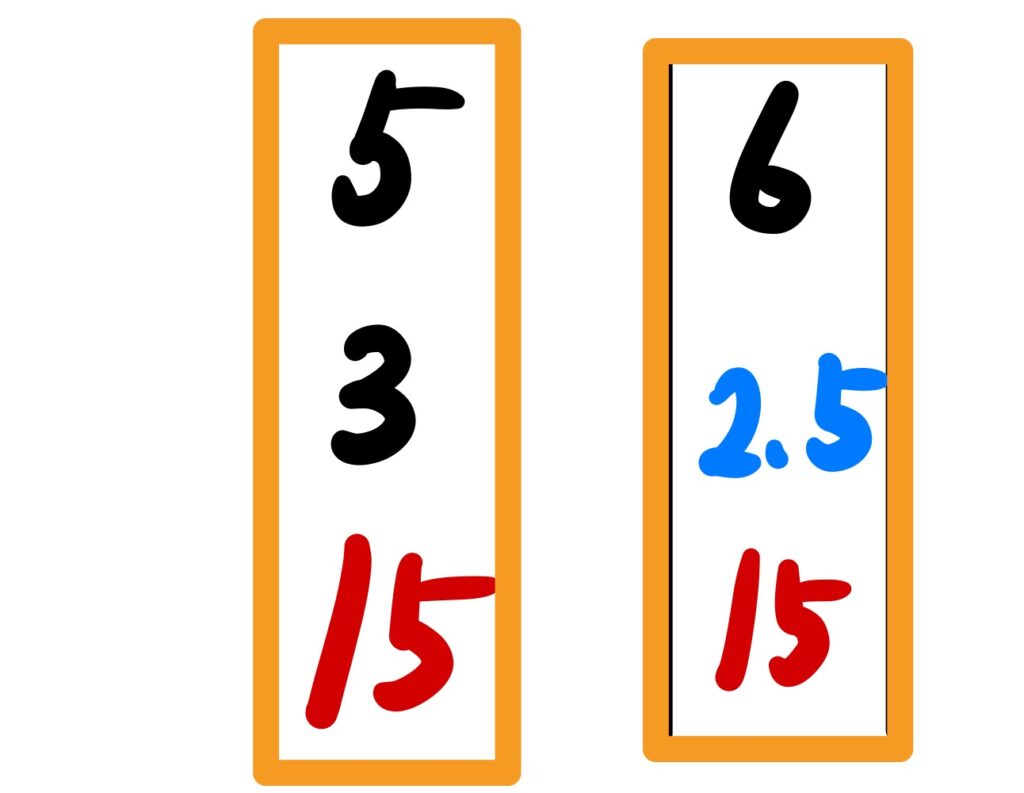
赤 5×3=15㎠
青 6×2.5=15㎠
と、同じ面積がありました。
何も珍しいことではなく、青を細かく見れば、1〜16㎠まで全て存在するのです。

つまり、紐の長さが違っても、同じ面積は存在することが多いということです。
①周りの長さが同じでも面積は変わる
②周りの長さが違っても同じ面積はある
勘違いしがちな面積のトリックですね。算数の世界はおもしろいですね。
それでは、ありがとうございました。

コメント