こんにちは、金輪際ポコ次郎です。
日本を世界一、算数好きな国にするために毎日頑張っています。

無限の彼方へいざ!

それやばい気がする
さて、突然ですが問題です。
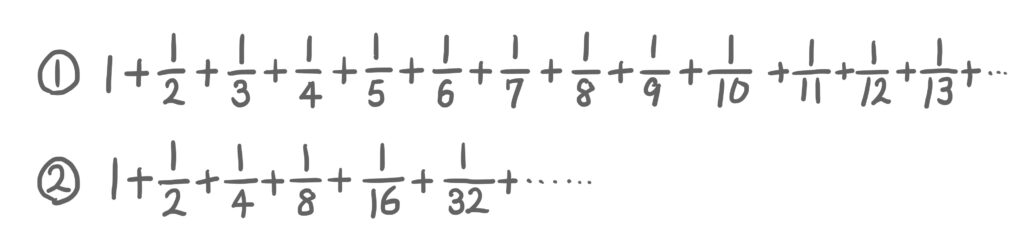
①、②のようにたし算をずーっと続けていきます。
それぞれの答えはどうなるでしょうか?

今回は無限の足し算を
考えるのじゃ

ずーっと足し続けるの?
無限に続くとどうなる?
①は無限に伸びる?
まずは、①の計算を考えてみましょう。
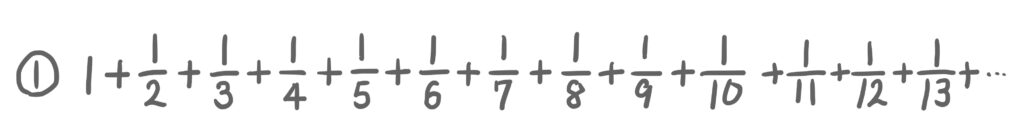

答えはどのくらいに
なると思う?

ぜんぜん想像も
できないよ?
式だけで見ると、答えを想像することは難しいですね。
こんなときは、式を図と結びつけることが一つの考え方です。
試しに、長さで考えてみましょう。

1mのリボンに、1/2m、1/3mのリボンを横に繋げていきます。これをずーっと繋げていくのです。

繋がるリボンはどんどん
短くなっていくけど…

ずーっと繋げていくと、この
長さは何千万m、何億mとなる
たす数はどんどん小さくなっていきますが、答えは無限に大きくなっていきます。
塵も積もれば山となる。
小さな数でも無限に足すと、♾️になるのです。
②も無限に伸びる?
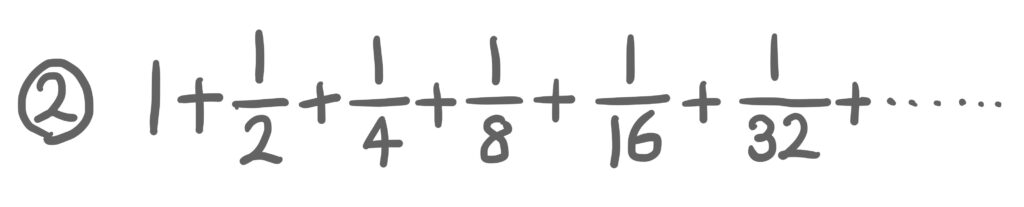

それならさ、
②も無限だよね

果たしてそうかのう?

いやいや、②も無限に足すん
だから、無限になるでしょ。

②の答えは2じゃ

…え!?
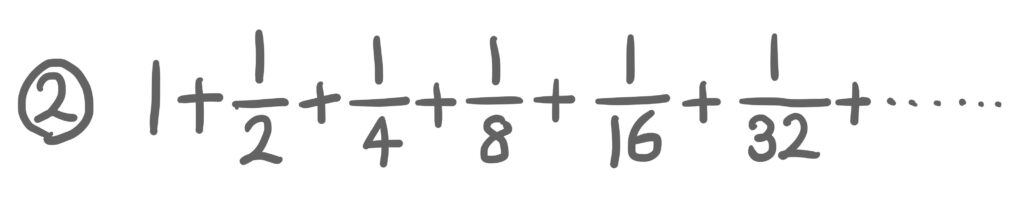
②は、①のように数を無限に足していますが、答えは♾️にはなりません。それどころか、答えはたったの2です。
なぜでしょうか。
これも、図で考えてみましょう!
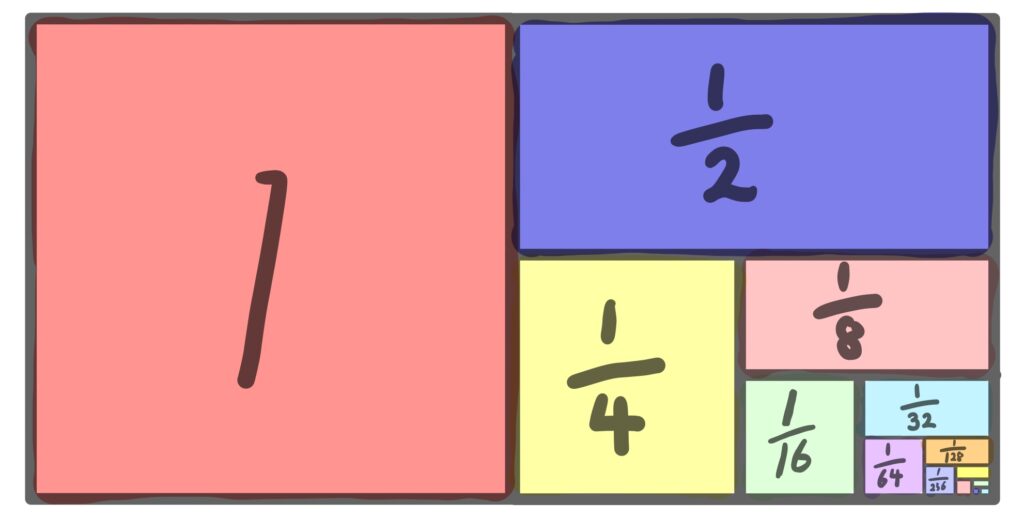
1/2+1/4+1/8+1/16+…は、それぞれが前の数の半分になっています。
これを示したのが上の図です。
このように考えてみると、半分に半分に、どんどん小さくなっていきます。無限に半分になっていくと、無限に足しても1を越えないのです。
そのため、
1+1/2+1/4+1/8+1/16+…
=1+1
=2
となります。
まとめ
今回は、2つの無限に足す計算を考えました。


②は無限にならなくて、
2になるのが意外だったよ

②も無限になりそうという
イメージをぶっ壊してきたのう
頭の中のイメージと異なるおもしろい問題でした。
無限にはまだまだ人間のわからないことがたくさんあります。
ぜひ、無限の世界に想いを馳せてみて下さい。
それでは、ありがとうございました!

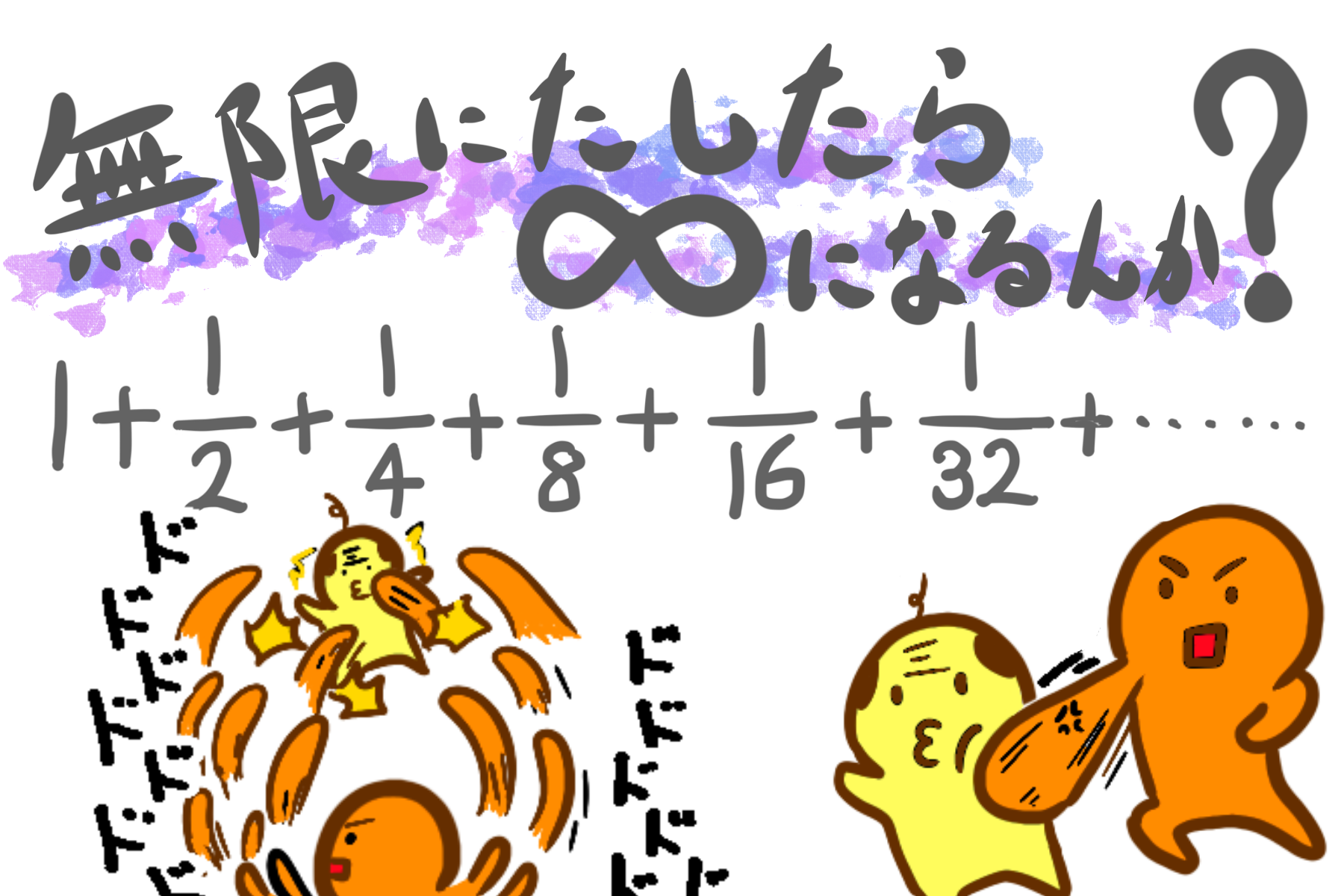

コメント