こんにちは、金輪際ポコ次郎です。
日本を世界一、算数好きな国にするために毎日頑張っています。

最近、寒いけど
頑張るのじゃ
今日はこんな問題を紹介します。
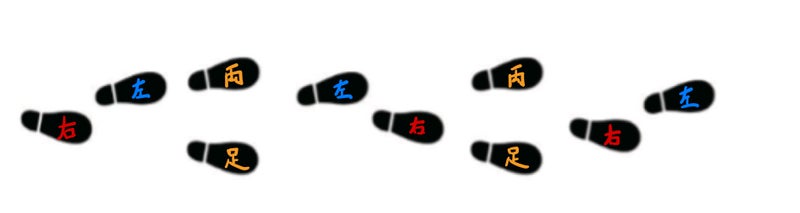
少し複雑なけんけんぱです。
右→左→パッ(両足)→左→右→パッ(両足)→右→左→
…と続いていきます。
さて、725歩目はどの足でしょうか?
右足?
左足?
両足?

725歩なんて
無理すぎん?
早速、考えていきましょう!!
725歩目はどの足か?

けんけんぱをしよう!

さて、どのように
考えるかじゃが…

よーし!
けんけんぱしよう!

ええ?
まずはけんけんぱを725回してみましょう!
けんけんぱ、けんけんぱ、けんけんぱ…

こ…これ725歩って
やばいね

725歩目にたどりつくまでには、ワシの膝は折れ、筋肉は断裂、医者には見放された上に生死の境をさまよい、一命を取り留めたとしても重度の後遺症に繋がることじゃろう。

おじいちゃん命懸けだね

懸けたくないわい!!
どうやら、725歩けんけんぱをやることは現実的ではありません。

「じゃあそもそも、この問題いらないじゃん」
と、つっこまれてしまいそうですが、算数を考える理由はただ一つ、おもしろいからです。
ぜひ、一緒に楽しんで考えていきましょう。
わり算で考えると…?

計算で考えることもできるのじゃ

へぇ、けんけんぱも計算か
①725÷3で考える
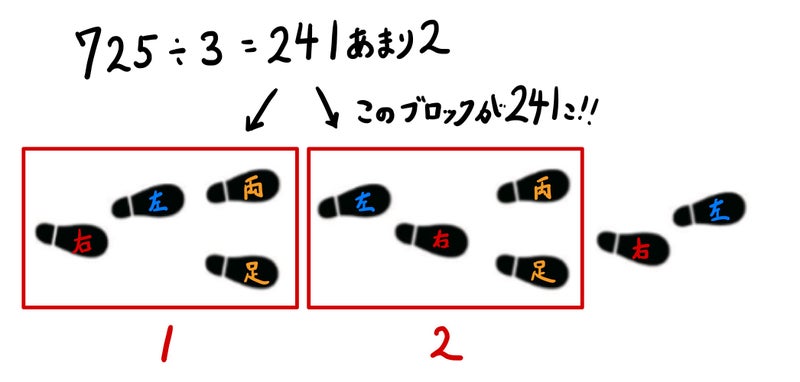
右→左→両足の3歩を1ブロックと考えます。
すると、725歩は
725÷3=241あまり2
241ブロックと、残り2歩
とわかります。

おお!一気に残り2歩へ
ワープしたね!!!

ワープ最高じゃ!

2歩進んだ足を調べ…
ん?

のこり2歩って、
右足から?
左足から?
迷ってしまいました。
右からなの?左からなの?
それがわからなければこの先には進めません。

まさに立ち往生じゃ!
ワシは大往生したい!
②725÷6で考える
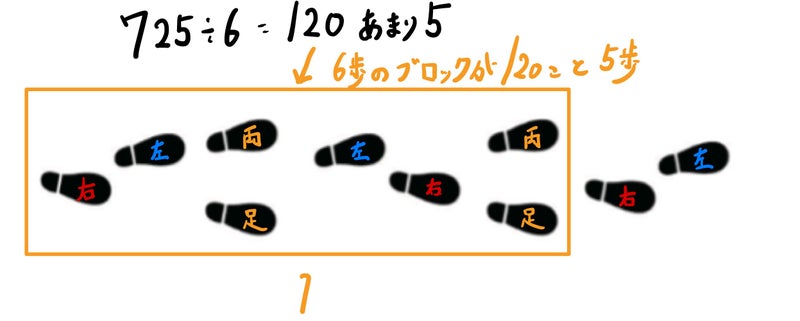
6でわると、6歩のブロックが120ことわかります。
残りの5歩で725歩です。

また右足か左足かどっちの
スタートかわからないんじゃ?

6のまとまりなら大丈夫じゃ
これは、3でわったときと同じように見えて、同じではありません。

なんと、次の一歩は必ず右足だとわかります!
これはただの一歩ではありません。
人類にとっても重要な一歩なのです。

すごい!
6歩で一周期だったのか!
右→左→両足→左→右
725歩目は右足だとわかりました!!
きまりをみつける
偶数、奇数、倍数
最後に、表を使ってきまりを見つける方法を紹介します。
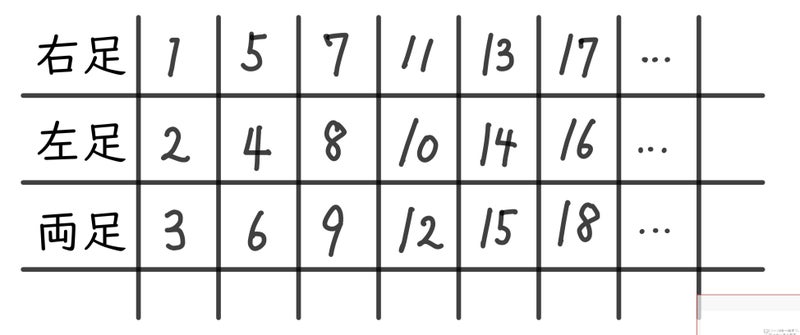
足と歩数の関係を表にまとめるとおもしろいことがわかります。
まず、1、3、5列目は順番に数が並びますが、2、4、6列目は違います。
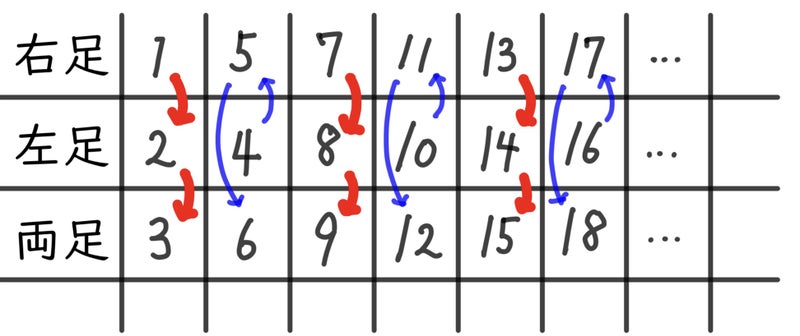

順に表をかいてみると
おもしろいのじゃ
また、奇数と偶数、倍数の観点で見ることもできます。
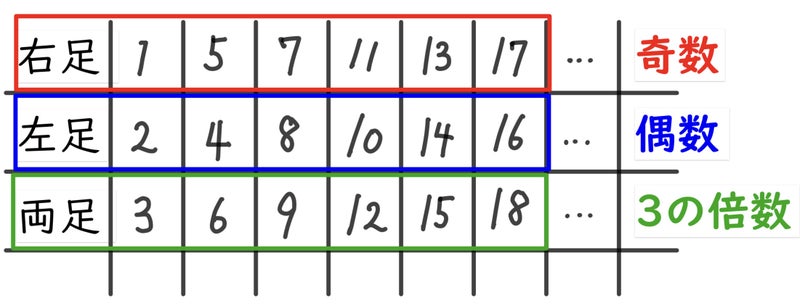
こうしてみると、
右足は奇数
左足は偶数
両足は3の倍数
とわかりますね!
725÷3=241あまり2ということは、奇数であって、3の倍数ではないことから、右足だとわかるのです!

3で割った考えも
役に立つんだね!!
剰余類
剰余類という考えを使うと、下のようになります。
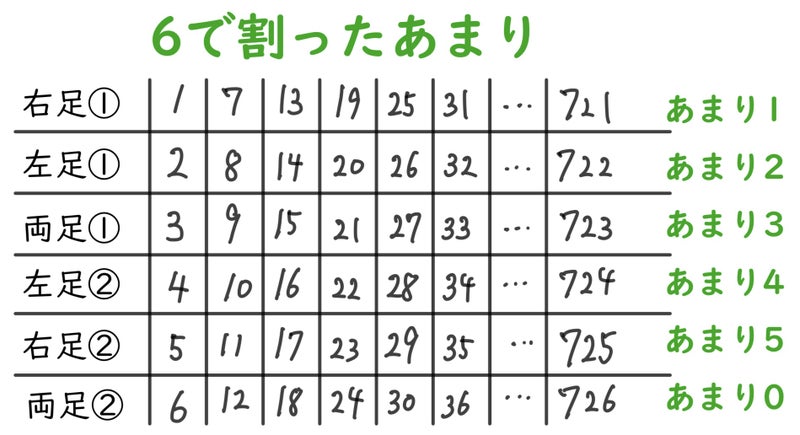
このようにみると、
725÷6=120あまり5
なので、右足だということがわかるのです。

一つの問題でも、いろいろな
考え方があるんだね

答えは一つでも、そこに
辿り着く道筋は自由なのじゃ!
寄り道かと思う解き方でも、素晴らしい発見につながることもあるのです。
ぜひ、算数という学びを楽しんでみてください。
それでは、ありがとうございました!
※当記事は「なにかと算数」の記事をもとに改変したものです。
こちらもよろしくお願いいたします!



コメント