円周率って4やで

こんにちは、金輪際ポコ次郎です。
日本を世界一、算数好きな国にするために毎日頑張っています。

さて、円周率です。

円周率は4やねん

円周率とは？

円周率とは割合です。

まず円があります。
この円が一周転がると、どこまで進むのか？

これは円が大きいほど遠くまで進めますね。

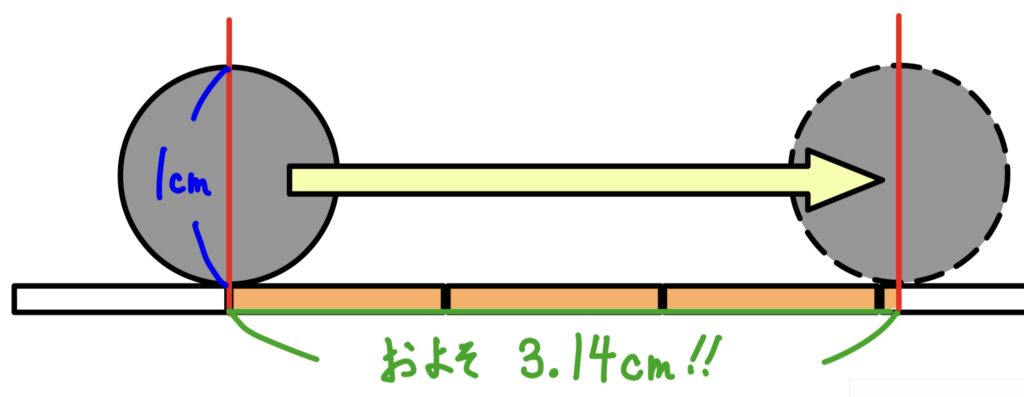
直径が1cmの円ならば、一周した時にちょうど3.14cm進みます。

直径が2cmならば6.28cm、直径が3cmならば9.42cmと、円が一周するときに進む距離は、ちょうど直径の3.14倍になります。

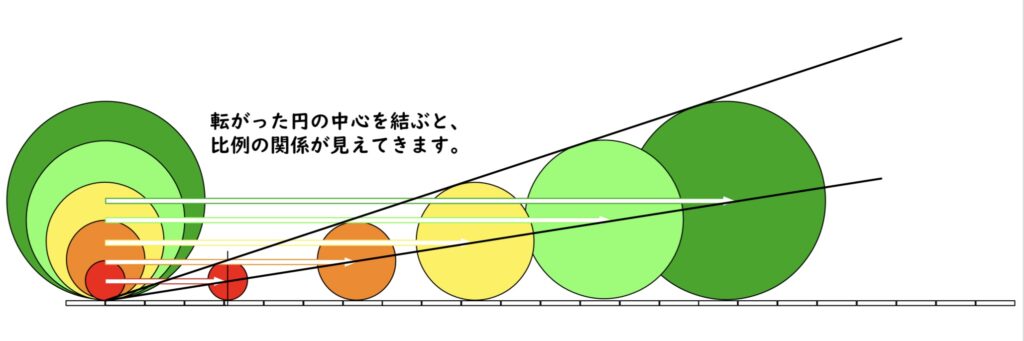
どれだけ円が大きくなっても、(円周の長さ)÷(直径)は必ず3.14になるわけです。

正確には、3.14159265358979･･･････と、この数はきまりがなく無限に続いていきます。小数でも分数にも表すことのできない無理数といわれています。

人類は太古からこの円の魅力に取り憑かれ、円周率の正確な値を調べてきました。

円周率は3か？

20年前の「ゆとり教育」では円周率を3で教えていたという報道がされました。

真偽はさておき、円周率が3であるかと聞かれると、偽です。

(周の長さ)÷(直径)＝3

となる図形は正六角形です。

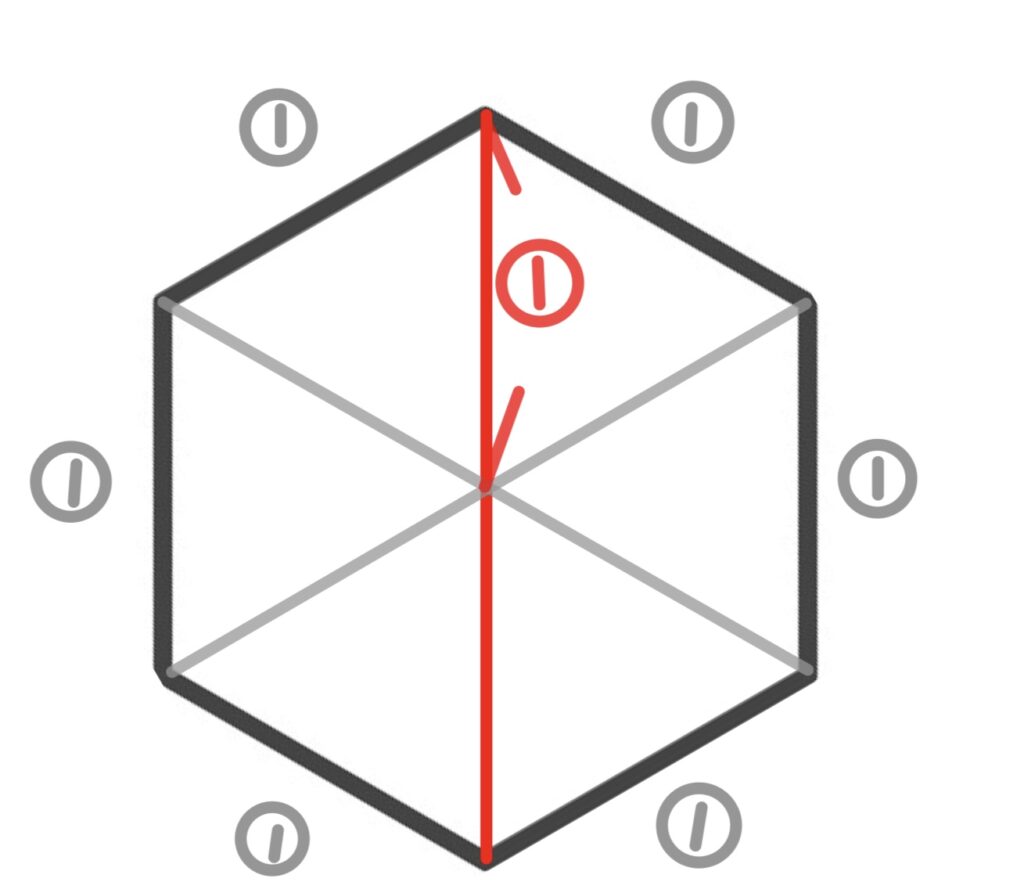
半径を1(直径は×2＝2)としたときの周の長さは6なので、

(周の長さ)÷(直径)＝3

そのため、円周率が3などというのはありえないのです。

もしも円周率が3ならば、車のタイヤは全て六角形になり、それはそれは揺れることでしょう。陸上トラックはカクカクに走りづらくなり、結婚指輪は5分つけていると指が痛くて離婚ということになりかねません。

円周率は4やねん

さて、ここから円周率が4であることの説明をしていきます。

円の半径をπとおきましょう。

そして、半径2cmの四分の一円を考えます。

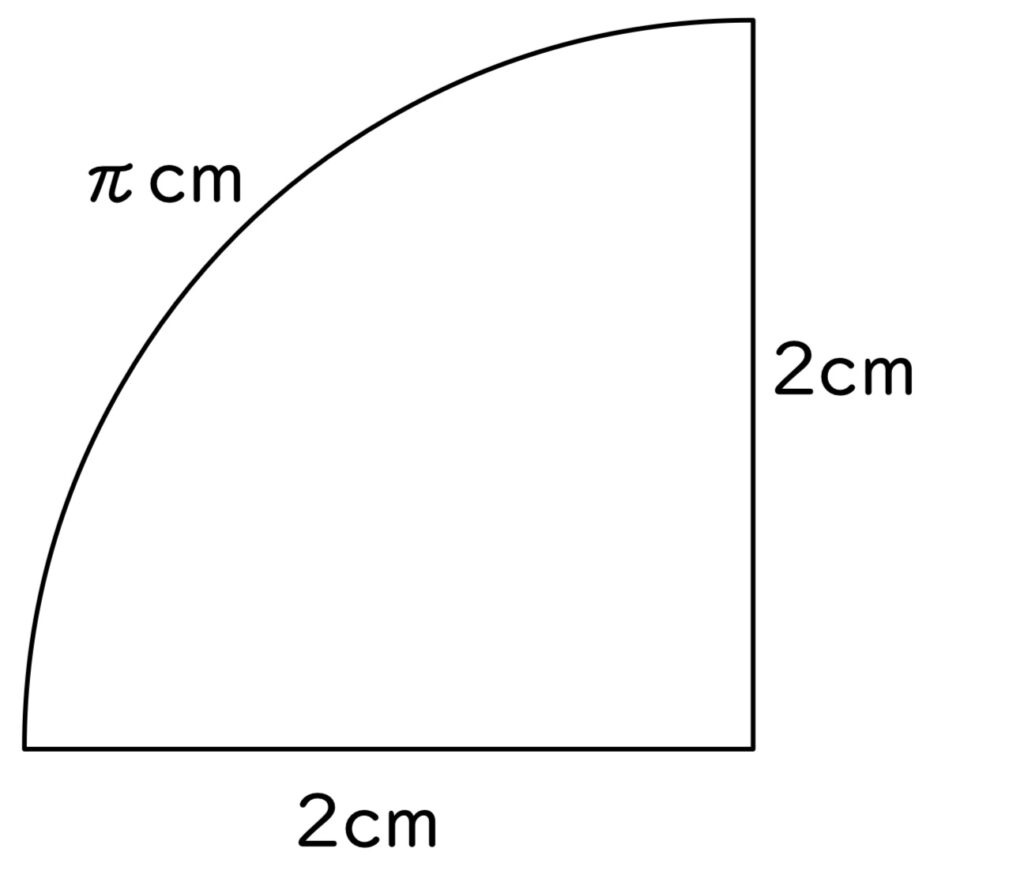
直径は4cmなので、円周は4×π＝4π

四分の一の弧の長さはちょうどπですね。

このπの長さを、直線で考えていきます。

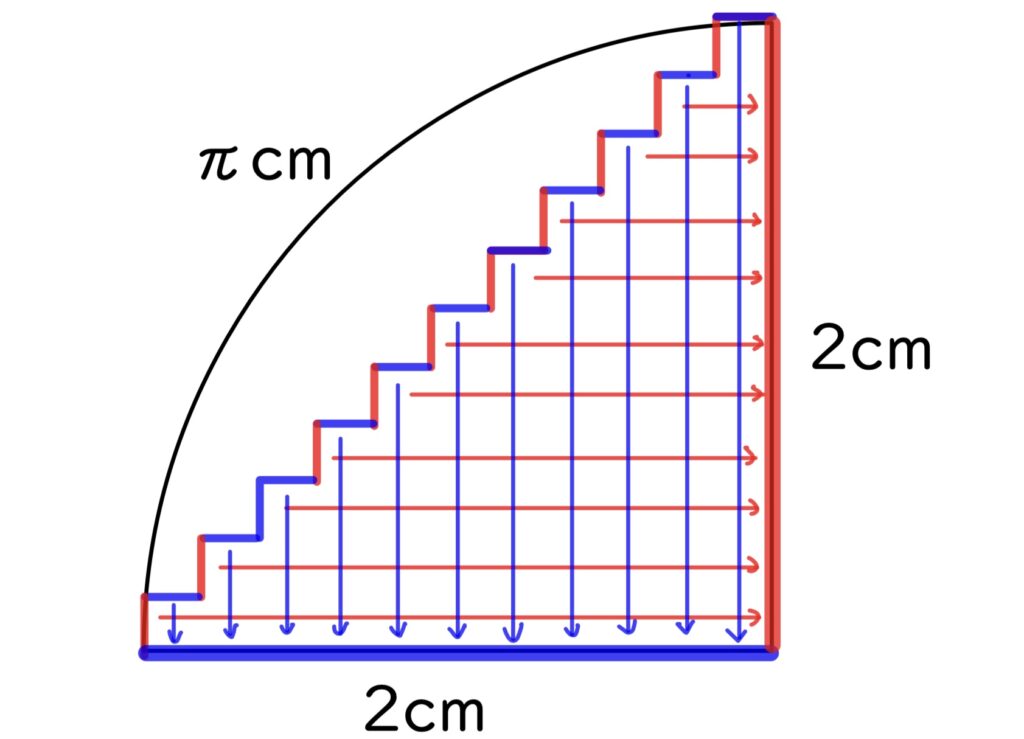
まず、上の図で考えると、赤青の階段部分の長さはそれぞれ2cmずつになりますよね。この階段の長さの合計は4cmだとわかります。

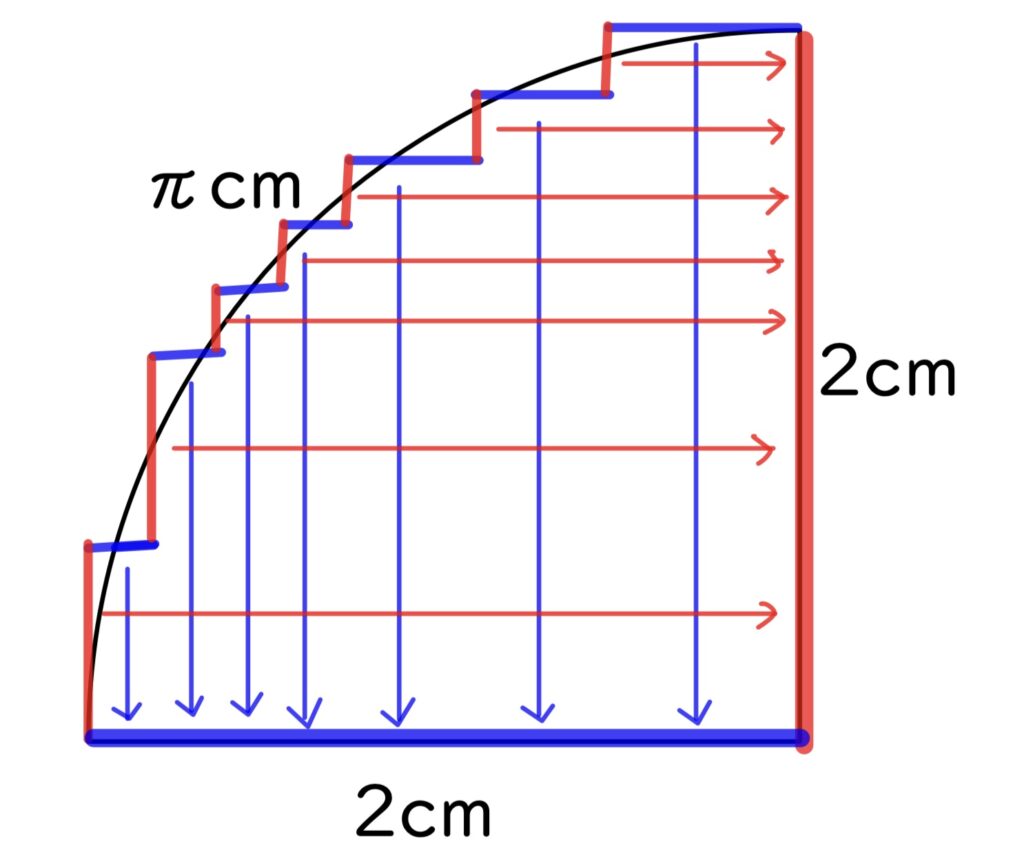
上の図は、だいぶπの長さに近くなります。
しかしこれでも、階段部分は4cmですね。

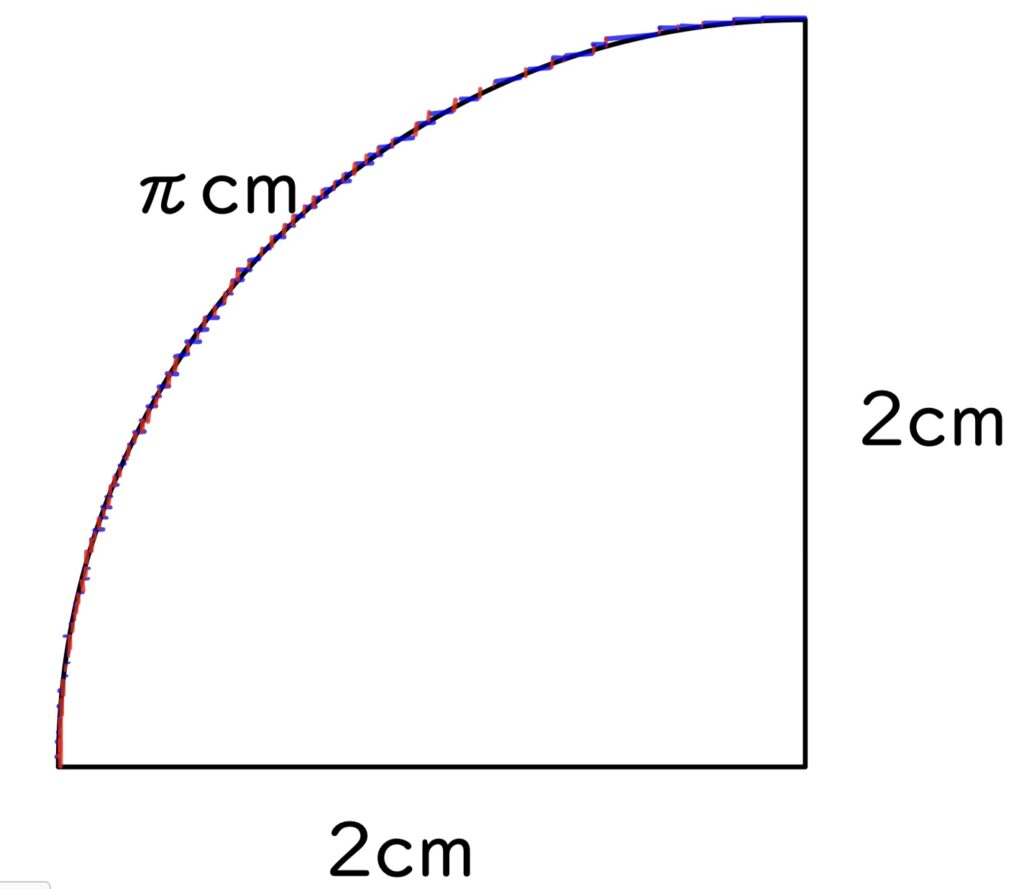
見えないほどに細かく、縦と横の線を無限に刻んでいきます。

これでも、縦の長さは2cm、横の長さは2cm、合計で4cmになります。

つまり、無限の世界で考えると、π＝4cm

円周率は4になるのです。

さて、今回は円周率が4になる理由を説明していきました。

本当は4ではないですが、なんだかちょっと納得してしまうような説得力がありましたね。

円周率の謎はまだまだ解明されていません。

あなたが、円周率を解く一人になるかもしれませんね。

それでは、ありがとうございました！