こんにちは、金輪際ポコ次郎です。
日本を世界一、算数好きな国にするために毎日頑張っています。
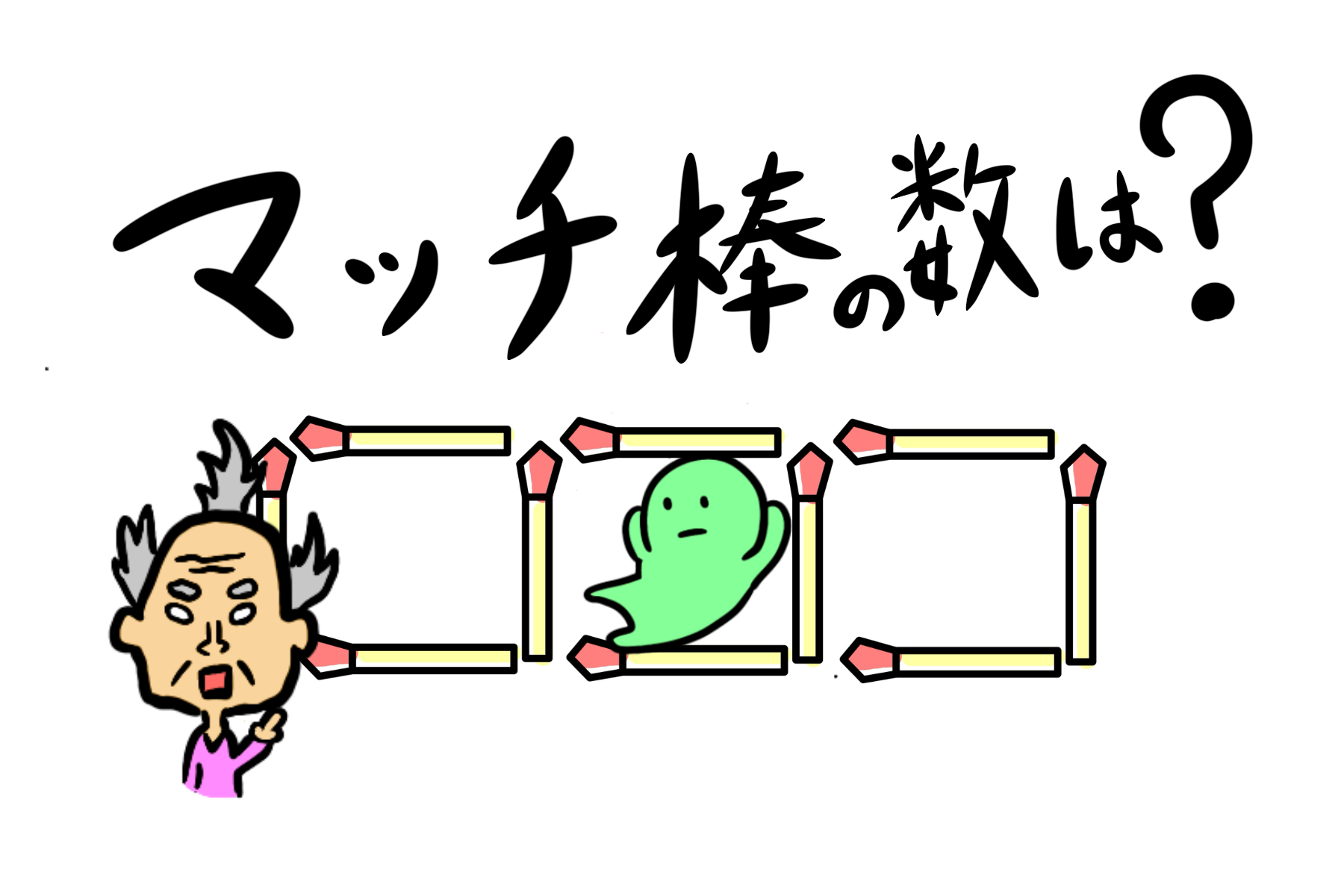
突然ですが、マッチ棒で正方形を作ってみました。
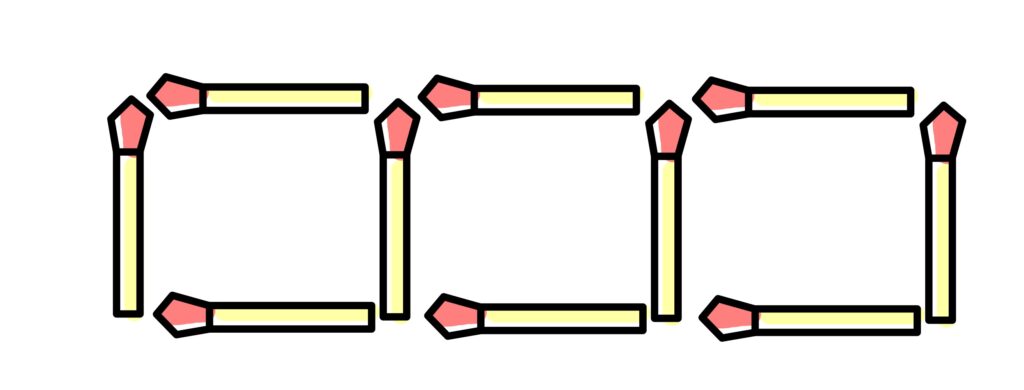
正方形を10こ作ったとき、
マッチ棒の本数はいくつでしょう。
中学受験でも有名なこちらの問題。泣き寝入りしていた人も多いと思います。しかし、これほど面白い問題もなかなかありません。
この記事を読むことで、
・マッチ棒を使った問題が得意になる。
・算数で大切な考え方がわかる。
・自信がつき、夜は眠れて肌ツヤもよくなる。
ことでしょう。
ぜひ、最後までご覧ください!

ぼくみたいな
もちもちつる肌
間違いない。

それはわからんが、
算数を楽しんでいこう。
マッチ棒の問題攻略!
正方形を作るんじゃ!
まずは正方形の問題を解決していきましょう。

目指せ!もち肌!

マッチ棒を横に繋げていきます。これで正方形を10こ作ります。

よし!
全部かこう!

なっ…!

どーん

1、2、3、4…
26、27、28……

…。

…ふぅ!
答えは31本だ!!!
答えは31本!
これでマッチ棒の問題はバッチリ!
夜も眠れてお肌ももちもちですね。
よかったよかった。
めでたしめでたし!

コラーー!!!

ぎゃーーー!!

勝手に終わるでない!
まだまだ方法はあるのじゃ!

やっぱり一本ずつ
数えるのはダメ…?

いや、むしろ根気あることじゃ。
他の面白い方法にも目を
向けることも大切じゃ。
数え上げて答えを出すことも素晴らしい方法です。問題を見た瞬間に諦めてしまうよりも、このように粘り強く考えることは大切なことだと思います。
マッチ棒の問題は、規則性を見つけることもおもしろいです。
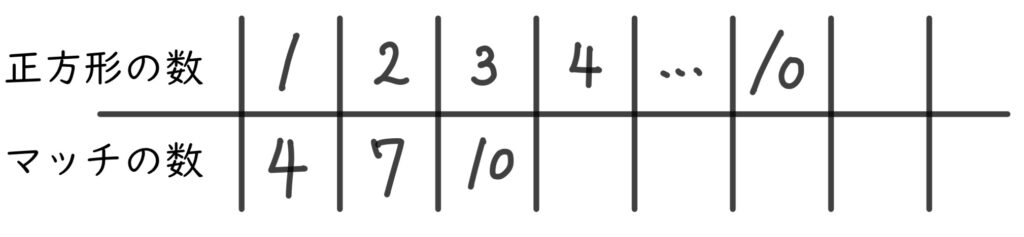
正方形とマッチ棒の関係を、表にまとめてみました。

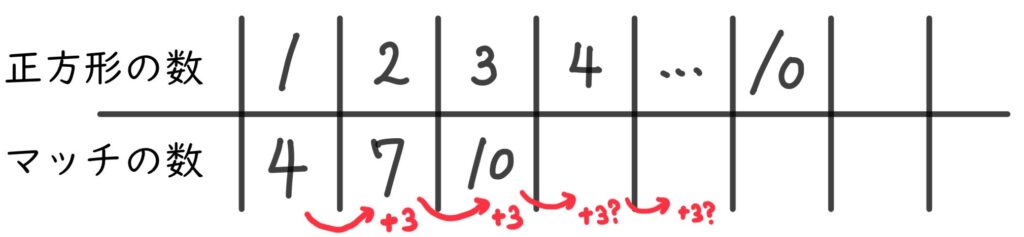
あれ?
3ずつ増えているよ?

うむ。それこそが
大切な気づきじゃ!
正方形作りに、最初は4本になりますが、2つ目以降は3本ずつ増えています。これは、正方形を作るときに前の正方形の1辺を利用しているからです。
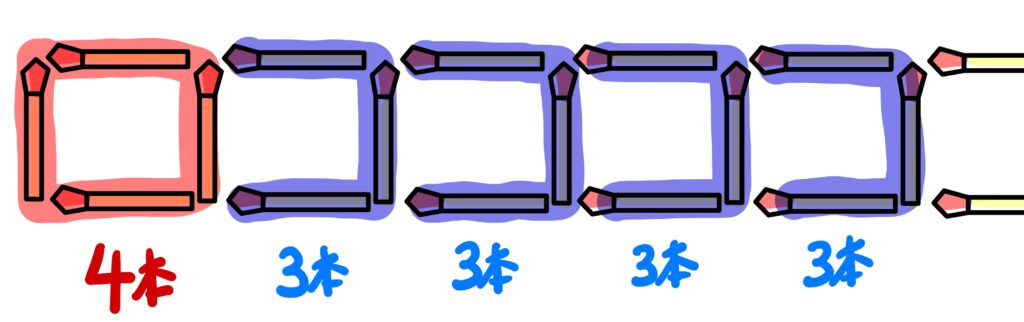

なるほど、だから3本ずつ
増えているんだね。

これで式にすることも
できるのじゃ
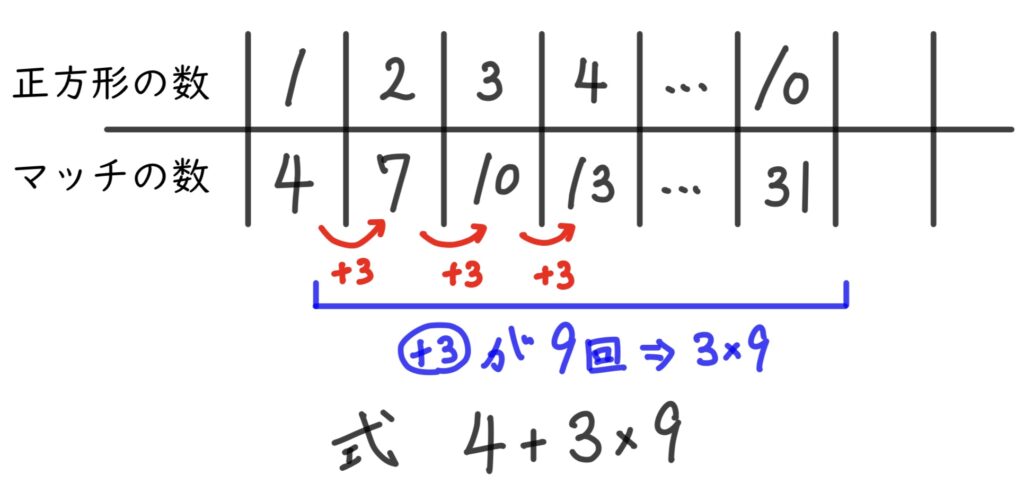
表にすると、マッチの数が3本ずつ増えていくことがわかります。
10個目まで、3は何回足されるのでしょうか。
4+3+3+3+3+3+3+……
10個目までは3が9回足されます。
このような計算は2年生で学びます。
かけ算です
3を9回足す→3×9とわかります。
よって、10個の正方形のマッチ棒の数は、
4+3×9
とわかりますね。ですが、9という数はどこから出てきたのでしょうか。9は、正方形が10個なら(10ー1)が3回足されると考えられます。そのため正確には
4+3×(10ー1)
という式がいいですね!
一般化するんじゃ!

これにて一件落着だね!

いや、まだ甘い。
例えばこうなるとどうじゃ!
正方形を100こ作ったとき、
マッチ棒の本数はいくつでしょう。

帰らせていただきます。
おせわになりました。

そう難しくはないのじゃ!
式を一般化するんじゃ!!!

いっぱんか??
正方形を求める式は
4+3×(10−1)
でした。
正方形の数が変わったとき、この式で
・変わるもの
・変わらないもの
を見てみましょう。
まず、4は変わりません。
最初の正方形はマッチ4本でできるからです。
+3も同じく変わりません。
2つ目以降の正方形は3本で作れます。
変わるのは、10です。
これは、正方形の数です。
正方形の数が100になったとき、
4+3×(100−1)=301
と計算できるのです。

おお!
こんなに一瞬で!

100個作らなくても
できるのう!

…あれ?
ばかにされてる?
もし、正方形を25こ作るときは、
4+3×(25−1)=76
正方形を48こ作るときは、
4+3×(48−1)=145
と計算できます。
つまり、正方形をマッチ棒で並べるときは、
4+3×(⬜︎の数ー1)
と示すことができます。これを一般化といいます。
こんな問われ方もあるんじゃ!
マッチ棒を124本使います
できる正方形はいくつでしょうか。
反対に、マッチ棒の数から正方形を求める問題です。

これも式がわかっていれば怖くない
4+3×(⬜︎の数ー1)=124
を計算すれば、⬜︎=41とわかります。
式を一般化することで、正方形が増えても、問題の出し方が変わっても計算で解くことができるんですね。
ぜひ、正方形のマッチ棒問題に挑戦し、成功と自己実現を叶えてください!
それでは、ありがとうございました!


コメント