こんにちは、金輪際ポコ次郎です。
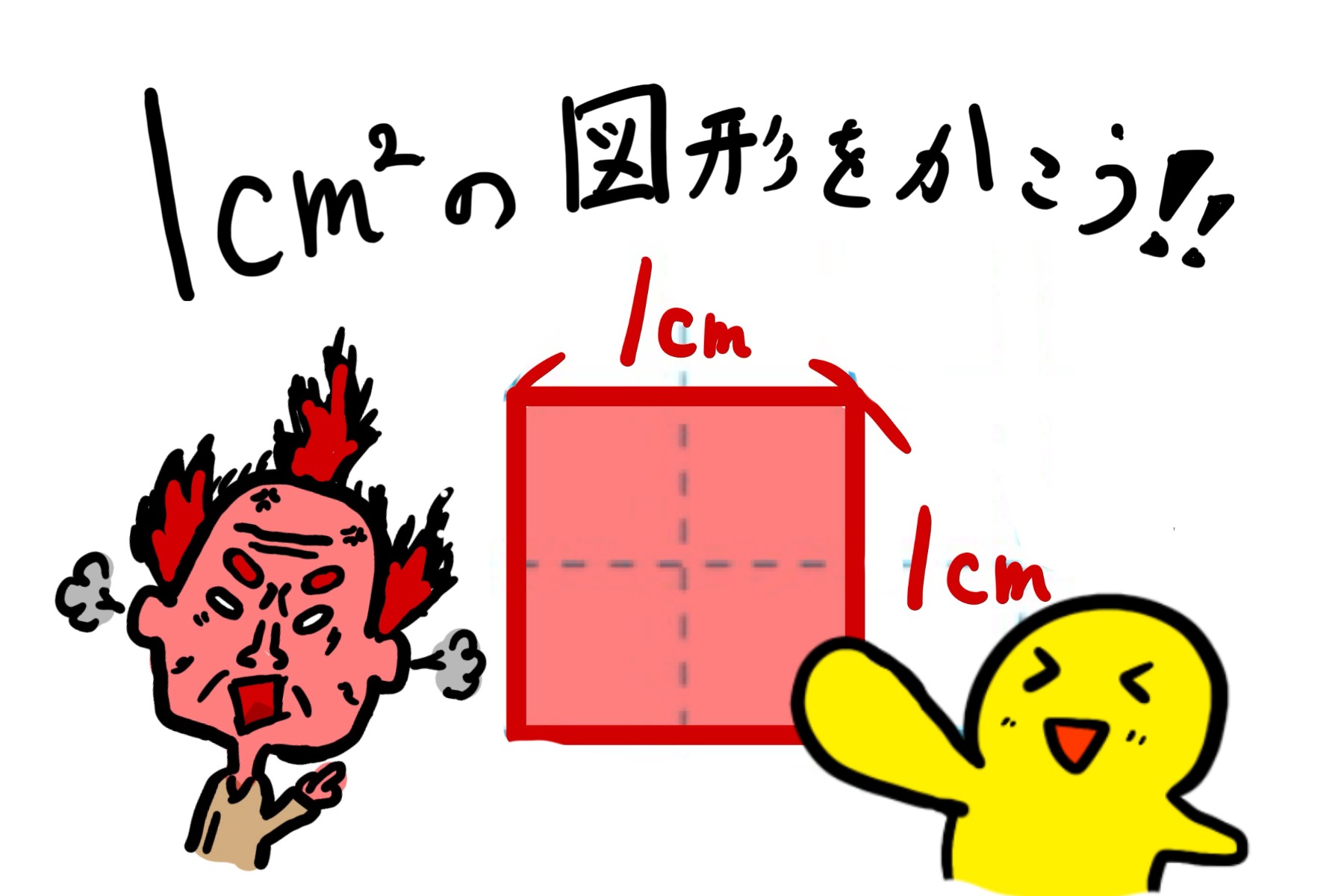
突然ですが、面積1㎠の図形を想像して下さい。
あなたが想像したのは、一辺が1cmの正方形ですね?


ボコ次郎
これがメンタリズムですじゃ

ましゅまろ
1㎠ってこれ以外
にもあるの?

ポコ次郎
形を変えるだけで、
まだまだあるのじゃ
今回は、1㎠という指先の広さを、算数の目で広げていきましょう。
まず、算数ノートは1㎠が4つに分かれています。つまり、ミニ四角形が4つあれば1㎠になります。
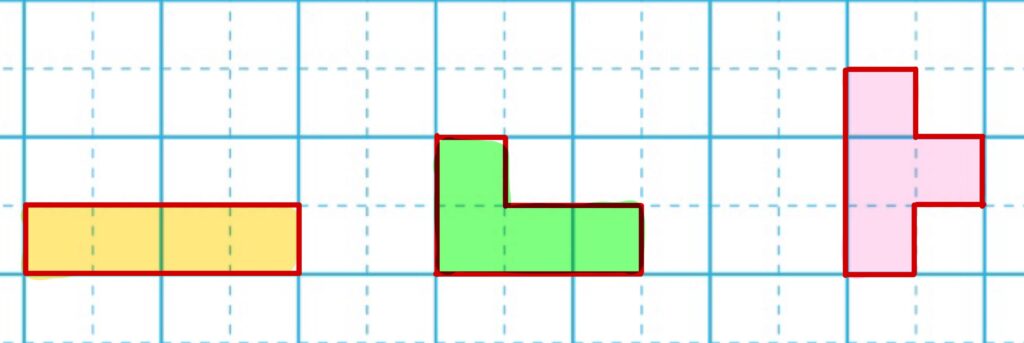
↑たとえばこんな感じです。これらは全て1㎠ですね。

ましゅまろ
本当に1㎠なの?

ポコ次郎
疑問を持つのはいいことじゃ
確かめてみよう。
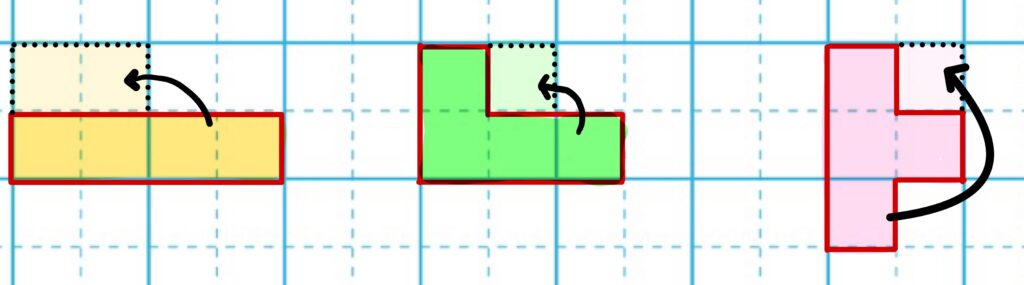
このように、切り取って移動させると元の正方形に戻ります。
これを等積移動(変形)といいます。
さて、他にも1㎠はできるでしょうか。
算数の世界を自由に歩き回ってみましょう。
1㎠の三角形や、平行四辺形を作ることもできます。
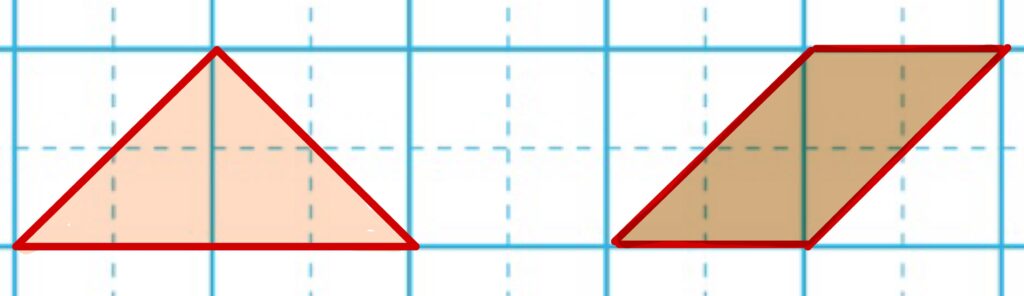
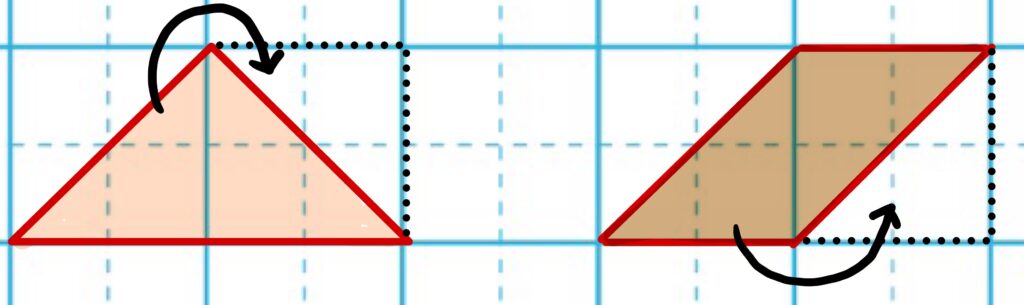
これは正方形を斜めに切って移動させています。
一辺が1cmの正方形だけでなく、色々な形ができるとわかってきましたね。まだまだ自由になります。例えば、六角形も作れます。
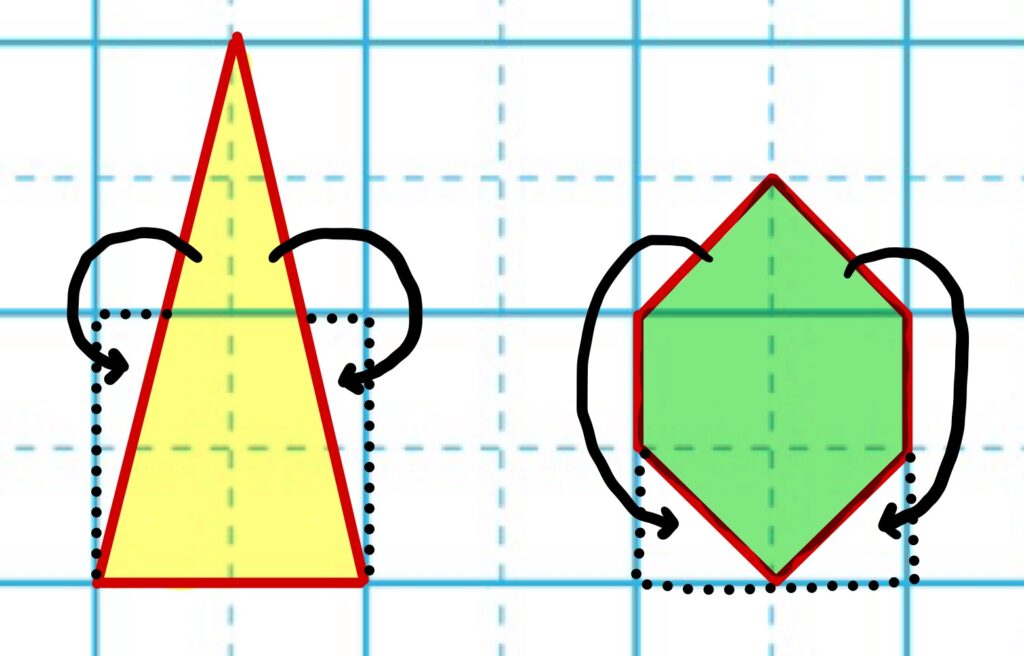
上の図形も、全て元の正方形を変形させたものです。1㎠はこんなに自由なのです。

ましゅまろ
おもしろいなぁ。
でも、円はできないでしょ?

ポコ次郎
円をもとに作ることもできるのじゃ

ましゅまろ
円もできるの!?
円をもとにして、次のような1㎠ができます。
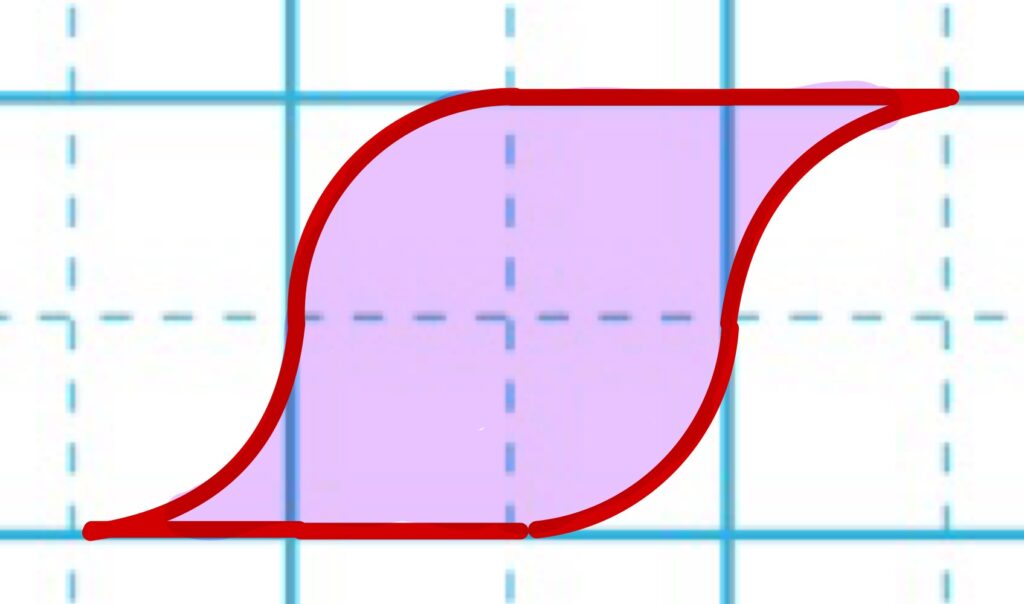
キャンディの包み紙型
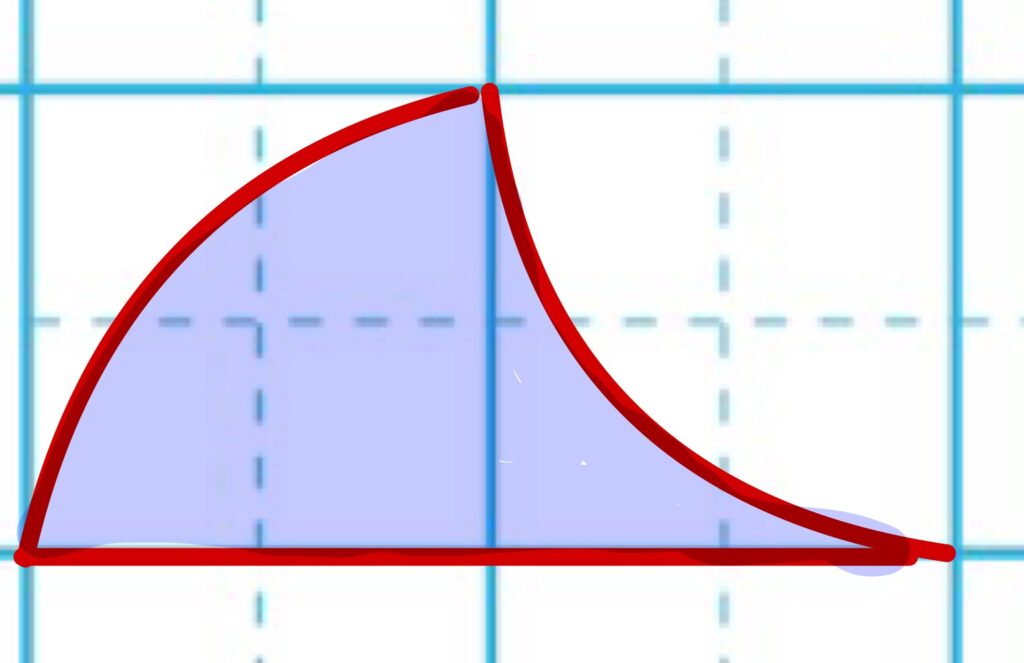
スリッパ型

ましゅまろ
1㎠には夢があるなぁー

ポコ次郎
おもしろいと思えたら
なによりじゃよ
このように、1㎠にじっくり目を向けるだけで、新しい発見はたくさんあります。等積移動などの高度な知識も体験的に身につくのでオススメです。ぜひ、他の様々な1㎠を考えてみてくださいね!
それでは、ありがとうございました!



コメント